Problem Statement

Given a string s, we are to find the number of substrings of size three that have distinct characters.

Theory

Subarray: A subarray is a contiguous sequence of elements within an array. It is essentially a subset of the original array, with elements taken from consecutive positions.

• Continuous parts of an array.
• Subarrays must maintain the order of elements from the original array.

For example, given an array [1, 2, 3, 4].

In general, for an array of size n, there are n*(n+1)/2 non-empty subarrays.

Below are all of the subarrays of the this array:

1. [1]
2. [1, 2]
3. [1, 2, 3]
4. [1, 2, 3, 4]
5. [2]
6. [2, 3]
7. [2, 3, 4]
8. [3]
9. [3, 4]
10. [4]

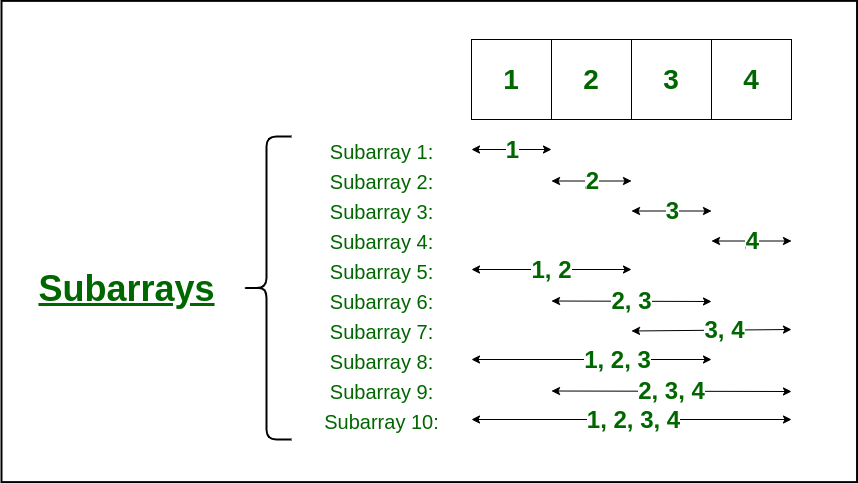
There are of different sizes.

If we are asked for the definite size of the subarray, like below are the subarrays of size 2:

1. [1, 2]
2. [2, 3]
3. [3, 4]

Substring: A substring is a continuous sequence of characters within a string. In other words, a substring is a part of a string.

• In the context of strings, subarrays are known as the substrings.
• Substrings are continuous parts of a string.
• Substrings must maintain the order of characters from the original string.

For example, in the string hello, some of the substrings are:

1. “h”
2. “he”
3. “hel”
4. “hell”
5. “hello”
6. “e”
7. “el”
8. “ell”
9. “ello”
10. “l”
11. “ll”
12. “llo”
13. “l”
14. “lo”
15. "o"

Examples

Example 1:

Input: s = “xyzzaz”

Output: 1

Explanation:

There are four substrings of size 3: “xyz”, “yzz”, “zza”, and “zaz”.

The only good substring of length 3 with characters is “xyz”.

Example 2:

Input: s = “aababcabc”

Output: 4

Explanation: There are 7 substrings of size 3: "aab", "aba", "bab", "abc", "bca", "cab", and "abc".

The good substrings are "abc", "bca", "cab", and "abc".

Different Approaches

1 Brute Force Approach

Intuition:

String:    x   y   z   z   a   z
Index:     0   1   2   3   4   5

Window:    x   y   z
Index:     0   1   2

1 For the first window [x, y, z], all characters are distinct, so we increment the count.

String:    x   y   z   z   a   z
Index:     0   1   2   3   4   5

Window:        y   z   z
Index:         1   2   3

2 For the next window [y, z, z], there is a repeated character z, so we don't increment the count.

String:    x   y   z   z   a   z
Index:     0   1   2   3   4   5

Window:            z   z   a
Index:             2   3   4

3 For the window [z, z, a], there is a repeated character z, so we don't increment the count.

String:    x   y   z   z   a   z
Index:     0   1   2   3   4   5

Window:                z   a   z
Index:                 3   4   5

4 For the window [z, a, z], there is repeated character z, so we don't increment the cout.

5. Final count = 1 and return it.

Algorithm:

1. Initialize a variable count to 0.
2. Iterate through the string s from index 0 to s.length() - 3.
   1. For each index i, consider the substring s[i:i+3].
   2. Initialize an unordered set chars to store characters in the substring.
   3. Initialize a boolean variable distinct to true.
   4. Iterate through the substring and check if each character is distinct.
   5. If any character is found to be repeated, set distinct to false and break out of the loop.
   6. If distinct is still true after the loop, increment count.
3. Return count, which represents the number of substrings of size three with distinct characters.

Code Implementation in C++:

#include <iostream>
#include <string>
#include <unordered_set>

using namespace std;

int countGoodSubstrings(string s) {
    int count = 0;

    // Iterate through the string from index 0 to s.length() - 3
    for (int i = 0; i < s.length() - 2; i++) {
        unordered_set<char> chars; // Use an unordered_set to store characters in the current window
        bool distinct = true; // Flag to check if all characters are distinct in the current window

        // Iterate over the current window of size 3
        for (int j = i; j < i + 3; j++) {
            // If the character is already present in the set, it's not distinct
            if (chars.find(s[j]) != chars.end()) {
                distinct = false;
                break;
            }
            chars.insert(s[j]); // Insert the character into the set
        }

        // If all characters in the window are distinct, increment the count
        if (distinct) {
            count++;
        }
    }

    return count; // Return the count of substrings with distinct characters
}

int main() {
    string s = "xyzzaz";
    cout << "Number of substrings of size three with distinct characters: " << countGoodSubstrings(s) << endl;
    return 0;
}

// OR


#include <iostream>
#include <string>
#include <unordered_set>

using namespace std;

int countGoodSubstrings(string s) {
    int count = 0;
    unordered_set<char> window;

    for (int i = 0; i < s.length() - 2; i++) {
        window.clear();
        window.insert(s[i]);
        window.insert(s[i + 1]);
        window.insert(s[i + 2]);
        if (window.size() == 3) {
            count++;
        }
    }

    return count;
}

int main() {
    string s = "xyzzaz";
    cout << "Number of substrings of size three with distinct characters: " << countGoodSubstrings(s) << endl;
    return 0;
}

Complexity Analysis:

Time Complexity:O(N^2), where n is the number of elements.

Space Complexity:O(1)

• We only use a constant amount of extra space.

2 Sliding Window Approach

Algorithm:

1. Initialize a variable count to store the number of good substrings.
2. Get the size of the string s and store it in variable n.
3. Iterate through the string s from index 0 to n - 3.
   1. For each iteration:
      1. Check if characters at indices i, i + 1, and i + 2 are distinct.
      2. If all characters are distinct, increment count.
4. Return the count, which represents the number of good substrings.

Code Implementation in C++:

#include <iostream>
#include <string>

using namespace std;

int countGoodSubstrings(string s) {
    int count = 0;          // Initialize count to store the number of good substrings
    int n = s.size();       // Get the size of the string

    // Iterate through the string from index 0 to n-3
    for(int i = 0; i <= n - 3; i++) {
        // Check if characters at index i, i+1, and i+2 are distinct
        if(s[i] != s[i + 1] && s[i] != s[i + 2] && s[i + 1] != s[i + 2]) {
            count++;         // If characters are distinct, increment count
        }
    }
    return count;           // Return the total count of good substrings
}

int main() {
    string s = "xyzzaz";
    cout << "Number of substrings of size three with distinct characters: " << countGoodSubstrings(s) << endl;
    return 0;
}

1. We initialize a variable count to store the number of good substrings.
2. We get the size of the string s using s.size() and store it in variable n.
3. We iterate through the string s from index 0 to n - 3.
4. For each iteration, we check if characters at indices i, i + 1, and i + 2 are distinct.
5. If all characters are distinct, we increment the count.
6. Finally, we return the count, which represents the number of good substrings.

Complexity Analysis:

Time Complexity: O(N)

• The time complexity of this approach is O(N), where N is the length of the string s. We iterate through the string only once.

Space Complexity: O(1)

• The space complexity is O(1), as we use only a constant amount of extra space regardless of the size of the input.