Problem Statement

Given the root node of a binary tree. Return true if the given binary tree is a binary search tree (BST) else false.

Examples

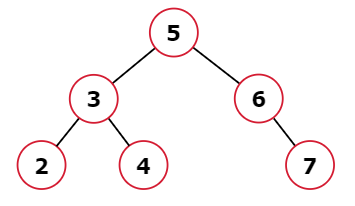
Example 1:

Input: root = [5, 3, 6, 2, 4, null, 7]
Output: true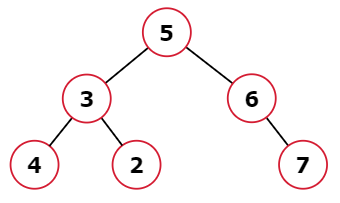

Example 2:

Input: root = [5, 3, 6, 4, 2, null, 7]
Output: false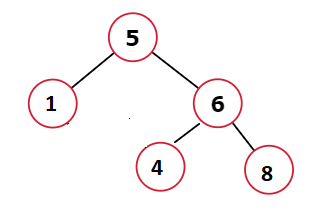

Example 3:

Input: root = [5, 1, 6, null, null, 4, 8]
Output: false

Explanation: The left node of subtree rooted at 6 has 4 which should be more than the 5.

Different Approaches

1️⃣ Recursion

Intuition:

To determine if a binary tree is a Binary Search Tree (BST), we need to ensure that for every node, its value falls within a specific range. This range is defined by the values of its parent nodes and their subtrees. For a node to be valid in a BST, all nodes in its left subtree must have values less than the node’s value, and all nodes in its right subtree must have values greater than the node’s value.

A straightforward way to approach this is to perform an inorder traversal of the tree, which will visit nodes in ascending order if the tree is a BST. By collecting node values in this order and then checking if this list is sorted, we can confirm whether the tree is a BST.

Approach:

1. Define a range for each node, every node must satisfy a range of valid values. The root node is initially allowed to have any value within the range from negative infinity to positive infinity.
2. Start with the root node and ensure its value is within the defined range.
3. Recursively validate the subtrees. For the left subtree of a node, update the range to be from negative infinity to the node’s value. For the right subtree of a node, update the range to be from the node’s value to positive infinity.
4. Ensure that each node’s value falls within its updated range. Recursively apply the same checks to the left and right children of each node.
5. If all nodes satisfy their respective ranges, the tree is a BST and if any node fails the check, the tree is not a BST.

Code:

#include <bits/stdc++.h>
using namespace std;

// Definition for a binary tree node.
  struct TreeNode {
      int data;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
  };
 

class Solution{
    public:
        bool isBST(TreeNode* root) {
            // Helper function to validate the BST
            return validate(root, LONG_MIN, LONG_MAX);
        }

    private:
        bool validate(TreeNode* node, long min, long max) {
            // Base case: if the node is null, return true
            if (node == nullptr) return true;
            
            // Check if the node's value falls within the valid range
            if (node->data <= min || node->data >= max) return false;
            
            // Recursively validate the left subtree
            // Update the max value to the current node's value
            bool leftIsValid = validate(node->left, min, node->data);
            
            // Recursively validate the right subtree
            // Update the min value to the current node's value
            bool rightIsValid = validate(node->right, node->data, max);
            
            // Both subtrees must be valid for the tree to be a BST
            return leftIsValid && rightIsValid;
        }
};

// Main method for testing
int main() {
    TreeNode* root = new TreeNode(7);
    root->left = new TreeNode(5);
    root->right = new TreeNode(10);
    root->left->left = new TreeNode(3);
    root->left->right = new TreeNode(6);
    root->right->left = new TreeNode(4);
    root->right->right = new TreeNode(15);
    
    Solution solution;
    std::cout << std::boolalpha << solution.isBST(root) << std::endl; // Output: false
    return 0;
}

Complexity Analysis:

• Time Complexity:O(N), Each node in the tree is visited once during the inorder traversal.
• Space Complexity:O(N), The recursive call stack can go up to the depth of the tree and the ans list can also store N elements in the worst case.