Problem Statement

Painter Partition:

You are given n boards, each with a certain length, and you need to paint them using k painters. Each painter can paint one board at a time and the time taken by a painter to paint a board is equal to the length of that board. The painters work simultaneously, and you want to minimize the maximum time any painter spends painting.

Objective: Find the minimum possible time (maximum time assigned to any painter) such that all the boards are painted.

Examples:

Example 1:
Input: boards = [10, 20, 30, 40], k = 2 (number of painters)
Output: 60

Explanation:
1) Painter 1 paints [10], Painter 2 paints [20, 30, 40], maximum of them = 90
2) Painter 1 paints [10, 20], Painter 2 paints [30, 40], maximum of them = 70
3) Painter 1 paints [10, 20, 30], Painter 2 paints [40], maximum of them = 60

Now we from all the possible cases we found the case 3 as the minimum
of them which is 60. So it is the minimum of maximum.

Example 2:

Input: boards = [10, 20, 30, 40, 50], k = 3
Output: 60

Explanation:
1) Painter 1 paints [10], painter 2 paints [20], painter 3 paints [30, 40, 50], So maximum is 120
2) Painter 1 paints [10, 20], painter 2 paints [30], painter 3 paints [40, 50], so maximum is 90
3) Painter 1 paints [10, 20], painter 2 paints [30, 40], painter 3 paints [50], so maximum is 70
4) Painter 1 paints [10, 20, 30], painter 2 paints [40], painter 3 paints [50], so maximum is 60

The minimum possible time with three painters is 60.

Split Array Largest Sum:

You are given an array of integers and a number m. You need to split the array into m contiguous subarrays such that the maximum sum among all subarrays is minimized.

Objective: Find the minimum largest sum possible after splitting the array into m subarrays.

Examples:

Example 1:

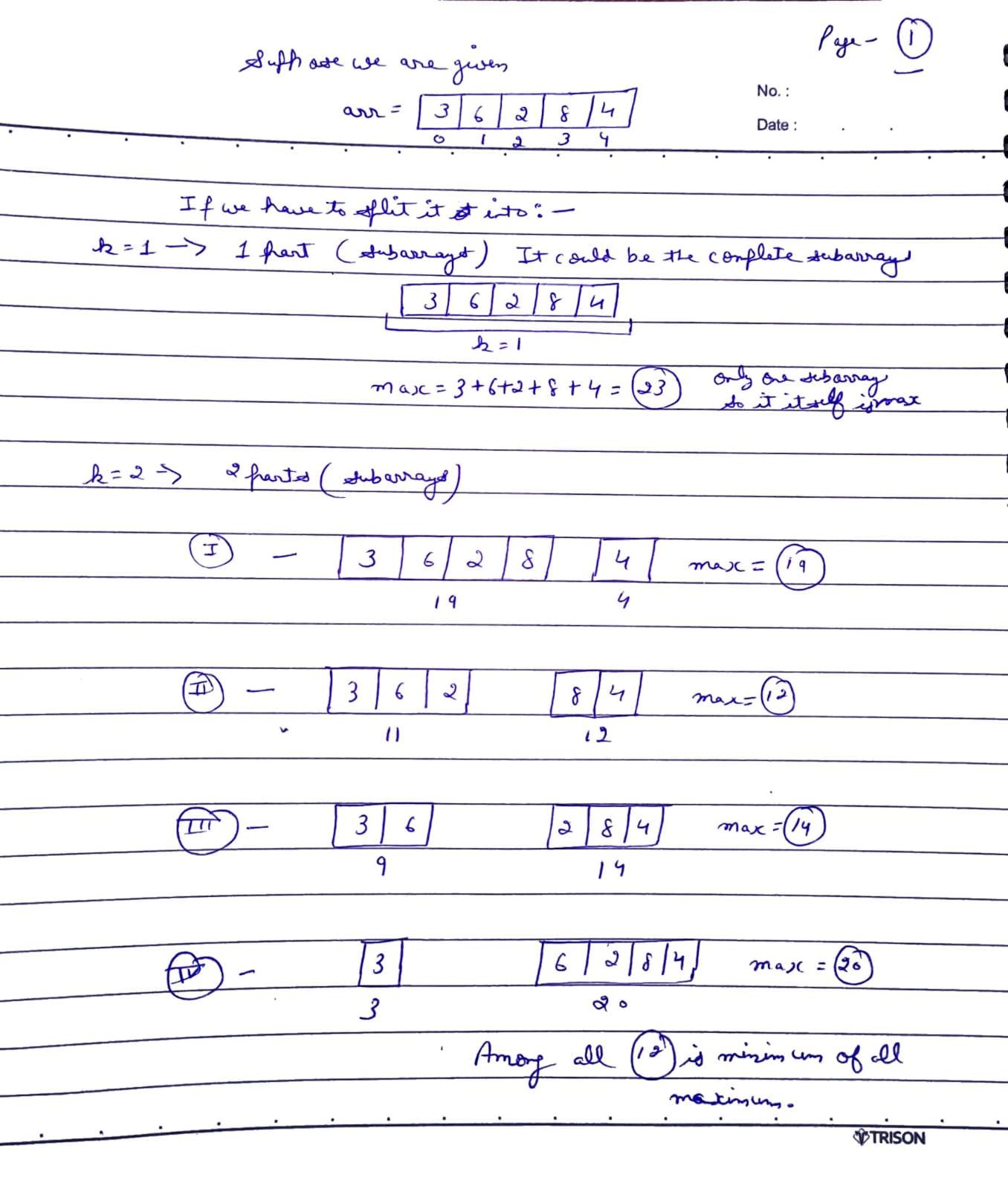
Input: arr = [7, 2, 5, 10, 8], k = 2
Output: 18

Explanation:
It can be split into below subarrays:
[7], [2, 5, 10, 8], maximum = 25
[7, 2], [5, 10, 8], maximum = 23
[7, 2, 5], [10, 8], maximum = 18
[7, 2, 5, 10], [8], maximum = 24

Out of all these possible combinations 18 is the minimum.

Example 2:

Input: arr = [3, 5, 1]
Output: 5

Explanation: There is only one way to split the array
into 3 subarrays, which is [3], [5], [1]
The largest among these subarrays is 5.

Different Approaches

1️⃣ Binary Search

Intuition:

The idea is to utilize the Binary Search algorithm to find the optimal solution for this problem. The search range for the problem is [max, sum], where max represents the maximum element of the array, and sum denotes the total sum of all elements in the array. This range is inherently sorted, allowing binary search to efficiently determine the appropriate half to explore in each iteration, thereby reducing the search space by half.
In this specific problem, the condition for eliminating one half of the search space is based on whether the number of partitions exceeds the given limit. If it does, it indicates that the current value of 'mid' is too small, so the left half is eliminated. Otherwise, the current 'mid' value is a potential answer, which is stored, and the search continues in the right half.

Approach:

Working of largestSubarraySumMinimized(arr,k):

1. Initialize two pointers low and high: Initially, low will point to maximum element of the array and high will point to the sum of all the elements of the array.
2. Intialize a while loop which will run till low is less than or equal to high. Calculate mid using the following formula: mid = (low+high) // 2 ( ‘//’ refers to integer division).
3. Use the countPartition() function to count the the number of partitions that can be made based on the potential value of ‘maxSum’, represented by the variable 'mid'.
4. If partitions is greater than k, it can be concluded that the number ‘mid’ is smaller than our answer. So, eliminate the left half and consider the right half(i.e. low = mid+1). Otherwise, the value mid is one of the possible answers. But the minimum value is needed, so, eliminate the right half and consider the left half(i.e. high = mid-1).
5. Finally, when the loop terminates, return the value of low as the pointer will be pointing to the answer.

Working of countPartitions(arr, maxSum):

1. Start with n = a.size(), which gives the number of elements in the vector a. Initialize partitions to 1, assuming at least one partition is required to cover all elements and also initialize subarraySum to 0, which will keep track of the sum of elements in the current subarray being considered.
2. Iterate in the array and check if adding the current element to subarraySum will keep the sum within the maxSum limit. If true, add it to the current. If adding current element would exceed maxSum, it indicates that current element should start a new subarray (partition). Increment the partitions counter to start a new partition. Reset subarraySum to a[i] to begin the new subarray with the current element.
3. After iterating through all elements in the array, return partitions, which represents the count of partitions needed.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to count partitions such 
    that each partition has sum <= maxSum*/
    int countPartitions(vector<int> &a, int maxSum) {
        int n = a.size();
        int partitions = 1;
        long long subarraySum = 0;

        for (int i = 0; i < n; i++) {
            if (subarraySum + a[i] <= maxSum) {
                // Add element to the current subarray
                subarraySum += a[i];
            } else {
                // Start a new subarray with current element
                partitions++;
                subarraySum = a[i];
            }
        }

        return partitions;
    }

public:
    /* Function to find the largest minimum
    subarray sum with at most k partitions*/
    int largestSubarraySumMinimized(vector<int> &a, int k) {
        
        // Initialize binary search boundaries
        int low = *max_element(a.begin(), a.end()); 
        int high = accumulate(a.begin(), a.end(), 0);

        // Apply binary search
        while (low <= high) {
            int mid = (low + high) / 2;
            int partitions = countPartitions(a, mid);

            if (partitions > k) {
                /*If partitions exceed k, increase 
                the minimum possible subarray sum*/
                low = mid + 1;
            } 
            else {
                /*If partitions are within k, try to
                minimize the subarray sum further*/
                high = mid - 1;
            }
        }

        /* After binary search, 'low' will 
        be the largest minimum subarray sum
        with at most k partitions*/
        return low;
    }
};

int main() {
    vector<int> a = {10, 20, 30, 40};
    int k = 2;

    // Create an instance of the Solution class
    Solution sol;

    int ans = sol.largestSubarraySumMinimized(a, k);
    cout << "The answer is: " << ans << "\n";
    return 0;
}

OR:

class Solution {
public:
    // Helper function to determine the minimum number of subarrays 
    // required if the maximum allowed sum of any subarray is `maxSumAllowed`.
    int getRequiredSubarrays(vector<int> &nums, int maxSumAllowed) {
        int subarrayCount = 1; // Start with at least one subarray.
        int currentSum = 0;

        for (int i = 0; i < nums.size(); i++) {
            if (currentSum + nums[i] <= maxSumAllowed) {
                currentSum += nums[i]; // Add the current element to the ongoing subarray.
            } else {
                currentSum = nums[i]; // Start a new subarray.
                subarrayCount++;
            }
        }
        return subarrayCount;
    }

    // Function to find the minimum possible largest sum among `k` subarrays.
    int minimizeLargestSubarraySum(vector<int> &nums, int k) {
        int maxElement = INT_MIN; // Maximum single element in the array.
        int totalSum = 0;         // Total sum of all elements in the array.

        // Calculate the maximum element and the total sum of the array.
        for (int i = 0; i < nums.size(); i++) {
            maxElement = max(maxElement, nums[i]);
            totalSum += nums[i];
        }

        // Binary search range: from the largest single element to the total sum.
        int low = maxElement;
        int high = totalSum;

        while (low <= high) {
            int mid = low + (high - low) / 2; // Midpoint of the current range.

            // Check if we can divide the array into `k` or fewer subarrays
            // such that the maximum sum of any subarray is `mid`.
            int requiredSubarrays = getRequiredSubarrays(nums, mid);

            if (requiredSubarrays <= k) {
                // If it's possible, try to minimize the maximum sum further.
                high = mid - 1;
            } else {
                // Otherwise, increase the allowed maximum sum.
                low = mid + 1;
            }
        }

        // The smallest possible maximum sum when divided into `k` subarrays.
        return low;
    }
};

Complexity Analysis:

• Time Complexity: O(N * (log(sum - max) + 1)), where N is the size of the array, 'sum' is the sum of all array elements, and 'max' is the maximum element in the array. This complexity arises because binary search is applied within the range [max, sum], and the countPartitions() function is invoked for each value of 'mid'. Inside the countPartitions() function, a loop iterates N times for each call.
• Space Complexity: As no additional space is used, so the Space Complexity is O(1).