Problem Statement

Given an array arr of n integers, where arr[i] represents price of the stock on the ith day. Determine the maximum profit achievable by buying and selling the stock any number of times.

Holding at most one share of the stock at any given time is allowed, meaning buying and selling the stock can be done any number of times, but the stock must be sold before buying it again. Buying and selling the stock on the same day is permitted.

Examples

Example 1:

Input: arr = [9, 2, 6, 4, 7, 3]
Output: 7

Explanation: Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6 - 2 = 4. Then buy on day 4 (price = 4) and sell on day (price = 7), profit = 7 - 4 = 3. Total profit = 4 + 3 = 7.

Example 2:

Input: arr = [2, 3, 4, 5, 6]
Output: 4

Explanation: Buy on day 1 (price = 2) and sell on day 5 (price = 6), profit = 6 - 2 = 4. Total profit is 4.

Different Approaches

1️⃣ Recursive Approach

Upon observation we find that every day, there will be two choices, either to do nothing and move to the next day or to buy/sell (based on the last transaction) and find out the profit. Therefore we need to generate all the choices in order to compare the profit. As we need to try out all the possible choices, we will use recursion.

Steps to form the recursive solution:

• Express the problem in terms of indexes: We need to consider the number of days, so one variable will be the array index (let's call it 'ind'). Additionally, we need to adhere to the condition that a stock cannot be bought again until it has been sold first. Therefore, a second variable 'buy' is needed to indicate whether the stock can be bought or sold on a particular day.
  f(ind, buy) will give the maximum profit that can be generated from day 'ind' to day (n-1), where 'buy' tells that whether we need to buy or sell the stock at day 'ind'.
• Try out all possible choices at a given index: Every day, there will be two choices, either to buy/sell the stock(based on the buy variable’s value) or to do nothing and move on to the next day. As we need to generate all the choices, use the pick/non-pick technique to the same.
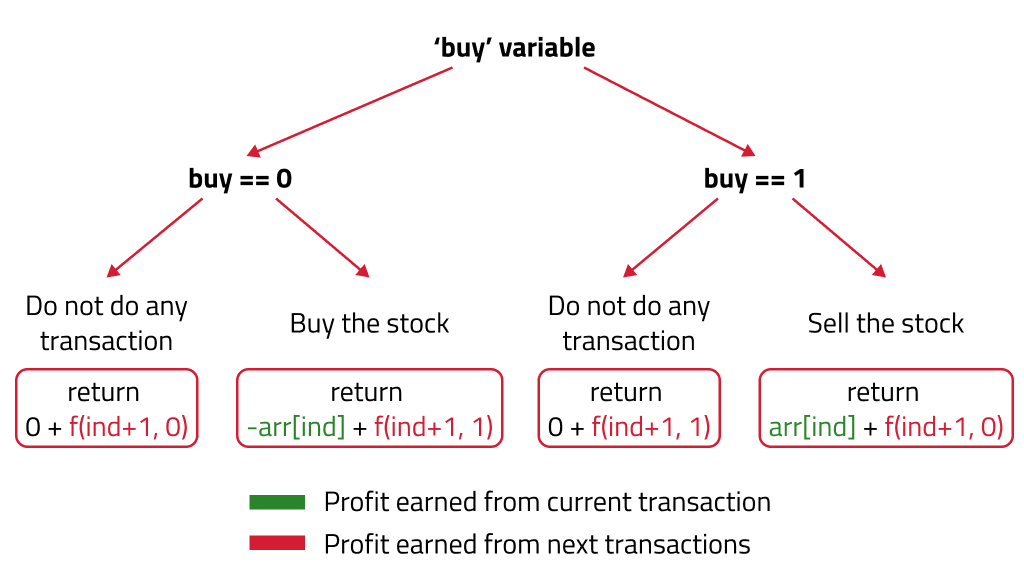
• Case 1: When buy == 0, the stock can be bought. If we can buy the stock on a particular day, there will be again two options:
  • Option 1: To do no transaction and move to the next day. In this case, the net profit earned will be 0 from the current transaction, and to calculate the maximum profit starting from the next day, we will recursively call f(ind+1,0). As we have not bought the stock, the ‘buy’ variable value will still remain 0, indicating that we can buy the stock the next day.
  • Option 2: The other option is to buy the stock on the current day. In this case, the net profit earned from the current transaction will be -arr[i]. As we are buying the stock, it means we are giving money out of our pocket, therefore the profit earned is negative. To calculate the maximum profit starting from the next day, we will recursively call f(ind+1,1). As we have bought the stock, the ‘buy’ variable value will change to 1, indicating that we can’t buy and only sell the stock the next day.
• Case 2: When buy == 1, means we are holding a stock, we can sell the stock. If we can sell the stock on a particular day, we will have two options:
  • Option 1: To do no transaction and move to the next day. In this case, the net profit earned will be 0 from the current transaction, and to calculate the maximum profit starting from the next day, we will recursively call f(ind+1,1). As we have not bought the stock, the ‘buy’ variable value will still remain at 1, indicating that we can’t buy and only sell the stock the next day.
  • Option 2: The other option is to sell the stock on the current day. In this case, the net profit earned from the current transaction will be +arr[i]. As we are selling the stock, we are putting the money into our pocket, therefore the profit earned is positive. To calculate the maximum profit starting from the next day, we will recursively call f(ind+1,0). As the stock has been sold, the ‘buy’ variable value will change to 0, indicating that we can buy the stock the next day.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, buy){
    // Base case here
    
    
    if(buy == 0){
    // buy
    	// do nothing and proceed to next
    	// index for buying.
        op1 = 0 + f(ind + 1, 0)
        
        // buy the current and proceed to next
        // index for selling
        op2 = -arr[ind] + f(ind + 1, 1)
    }
    if(buy == 1){
    // sell
    
    	// do nothing and proceed to next
    	// index for selling.
        op1 = 0 + f(ind + 1, 1)
        
        // sell the current one, make profit and
        // proceed to next index to buy again.
        op2 = arr[ind] + f(ind + 1, 0)
    }
           
}

• Take the maximum of all choices: As we are looking to maximize the profit earned, return the maximum value in both cases.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, buy){
    //Base case here
    
    
    if(buy == 0){
    // buy
    	// do nothing and proceed to next
    	// index for buying.
        op1 = 0 + f(ind + 1, 0)
        
        // buy the current and proceed to next
        // index for selling
        op2 = -arr[ind] + f(ind + 1, 1)
    }
    if(buy == 1){
    // sell
    
    	// do nothing and proceed to next
    	// index for selling.
        op1 = 0 + f(ind + 1, 1)
        
        // sell the current one, make profit and
        // proceed to next index to buy again.
        op2 = arr[ind] + f(ind + 1, 0)
    }
    
    // max of do nothing and buy/sell
    return max(op1, op2)    
}

• Base cases:
  • If ind == n, it means we have finished trading on all days, and there is no more money that we can get, therefore simply return 0. No more transactions to made.

Recursive Tree:

prices = [3, 2, 6, 5, 0, 3]

We start from day 0 with no stock (0, 0), and each step, evaluate all possible decisions recursively.

Legend:

• (i, holding):
  • i: Current day.
  • holding: 1 if holding stock, 0 otherwise.
• Decisions:
  • Buy: Subtract the current price from profit.
  • Sell: Add the current price to profit.
  • Skip or Hold: Move to the next day without a transaction.

(0, 0)  [Day 0, not holding]
├── Buy: (1, 1) --> Profit = -3
│   ├── Sell: (2, 0) --> Profit = -3 + 2 = -1
│   │   ├── Buy: (3, 1) --> Profit = -1 - 6 = -7
│   │   │   ├── Sell: (4, 0) --> Profit = -7 + 5 = -2
│   │   │   │   ├── Buy: (5, 1) --> Profit = -2 - 0 = -2
│   │   │   │   │   ├── Sell: (6, 0) --> Profit = -2 + 3 = 1
│   │   │   │   │   └── Skip: (6, 1) --> Profit = -2
│   │   │   │   └── Skip: (5, 0) --> Profit = -2
│   │   │   └── Hold: (4, 1) --> Profit = -7
│   │   └── Skip: (3, 0) --> Profit = -1
│   └── Hold: (2, 1) --> Profit = -3
│       ├── Sell: (3, 0) --> Profit = -3 + 6 = 3
│       │   ├── Buy: (4, 1) --> Profit = 3 - 5 = -2
│       │   │   ├── Sell: (5, 0) --> Profit = -2 + 0 = -2
│       │   │   └── Skip: (5, 1) --> Profit = -2
│       │   └── Skip: (4, 0) --> Profit = 3
│       └── Hold: (3, 1) --> Profit = -3
└── Skip: (1, 0) [Day 1, not holding]
    ├── Buy: (2, 1) --> Profit = -2
    │   ├── Sell: (3, 0) --> Profit = -2 + 6 = 4
    │   │   ├── Buy: (4, 1) --> Profit = 4 - 5 = -1
    │   │   │   ├── Sell: (5, 0) --> Profit = -1 + 0 = -1
    │   │   │   └── Skip: (5, 1) --> Profit = -1
    │   │   └── Skip: (4, 0) --> Profit = 4
    │   └── Hold: (3, 1) --> Profit = -2
    └── Skip: (2, 0) --> Profit = 0

Code:

class Solution {
public:
    /*
    Recursive function to calculate the maximum profit.
    @param prices - A vector containing the prices of the stock on different days.
    @param currentIndex - The current day index being processed.
    @param canBuy - A flag indicating whether buying is allowed (1 for buy, 0 for sell).
    @return Maximum profit that can be achieved from the current state.
    */
    int recursive(vector<int>& prices, int currentIndex, int canBuy) {
        // Base Case: If we reach the last day, no further transactions can be made
        if (currentIndex >= prices.size()) {
            return 0;
        }

        int doNothingProfit = 0; // Profit when no action is taken
        int transactionProfit = 0; // Profit when a transaction (buy/sell) is performed

        if (canBuy == 1) {
            // Buying is allowed

            // Option 1: Do nothing, move to the next day
            doNothingProfit = recursive(prices, currentIndex + 1, 1);

            // Option 2: Buy the stock, reduce the profit by the stock price, and switch to selling state
            transactionProfit = -prices[currentIndex] + recursive(prices, currentIndex + 1, 0);
        } else {
            // Selling is allowed

            // Option 1: Do nothing, move to the next day
            doNothingProfit = recursive(prices, currentIndex + 1, 0);

            // Option 2: Sell the stock, add the stock price to profit, and switch to buying state
            transactionProfit = prices[currentIndex] + recursive(prices, currentIndex + 1, 1);
        }

        // Return the maximum profit between doing nothing and performing a transaction
        return max(doNothingProfit, transactionProfit);
    }

    /*
    Function to calculate the maximum profit using recursive approach.
    @param prices - A vector containing the prices of the stock on different days.
    @param n - The total number of days (size of the prices array).
    @return Maximum profit that can be achieved.
    */
    int stockBuySell(vector<int> prices, int n) {
        return recursive(prices, 0, 1); // Start from day 0 with buying allowed
    }
};

OR:

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

int maxProfitRecursive(int index, bool holding, const vector<int>& prices) {
    // Base case: If we reach the end of the array
    if (index == prices.size()) {
        return 0;
    }

    // If not holding a stock
    if (!holding) {
        int buy = -prices[index] + maxProfitRecursive(index + 1, true, prices);
        int skip = maxProfitRecursive(index + 1, false, prices);
        return max(buy, skip);
    } else { // If holding a stock
        int sell = prices[index] + maxProfitRecursive(index + 1, false, prices);
        int hold = maxProfitRecursive(index + 1, true, prices);
        return max(sell, hold);
    }
}

int maxProfit(vector<int>& prices) {
    return maxProfitRecursive(0, false, prices);
}

int main() {
    vector<int> prices = {7, 1, 5, 3, 6, 4};
    cout << "Maximum Profit: " << maxProfit(prices) << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity: O(2^(N)), where N is the number of row. As, for each index, there are two possible options.
  • This is because each day has two choices (buy/sell or skip/hold), leading to an exponential number of recursive calls.
• Space Complexity: O(N), at maximum the depth of the recursive stack can go up-to N.

2️⃣ Memoization

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

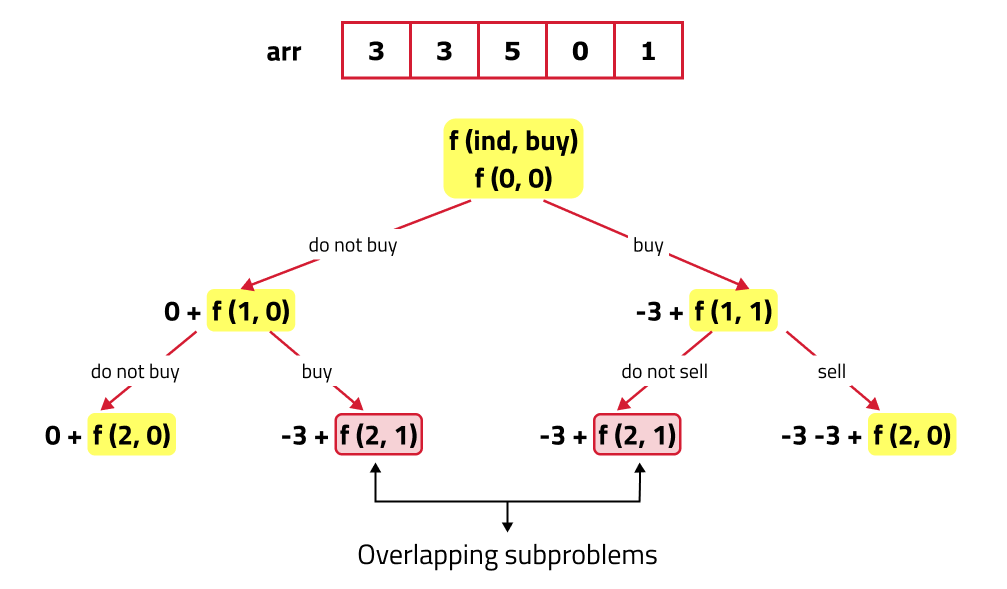
In order to convert a recursive solution to memoization the following steps will be taken:

• Declare a dp array of size [n][2]: As there are two changing parameters in the recursive solution, 'ind' and 'buy'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'buy' only two values possible 0, 1.
  • The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
• While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
• Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

Code:

#include <vector>
#include <iostream>
#include <cstring> // For memset
using namespace std;

// Helper function with memoization
int maxProfitMemo(int index, bool holding, const vector<int>& prices, vector<vector<int>>& dp) {
    // Base case: If we've reached the end of the prices array
    if (index == prices.size()) {
        return 0;
    }

    // If this state has been computed, return it
    if (dp[index][holding] != -1) {
        return dp[index][holding];
    }

    // If not holding a stock
    if (!holding) {
        int buy = -prices[index] + maxProfitMemo(index + 1, true, prices, dp);
        int skip = maxProfitMemo(index + 1, false, prices, dp);
        dp[index][holding] = max(buy, skip);
    } else { // If holding a stock
        int sell = prices[index] + maxProfitMemo(index + 1, false, prices, dp);
        int hold = maxProfitMemo(index + 1, true, prices, dp);
        dp[index][holding] = max(sell, hold);
    }

    return dp[index][holding];
}

// Main function
int maxProfit(vector<int>& prices) {
    int n = prices.size();
    vector<vector<int>> dp(n, vector<int>(2, -1)); // Initialize dp table with -1
    return maxProfitMemo(0, false, prices, dp); // Start from day 0 with no stock
}

int main() {
    vector<int> prices = {3, 2, 6, 5, 0, 3};
    cout << "Maximum Profit: " << maxProfit(prices) << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N*2), There are N*2 states, therefore at max ‘N*2’ new problems will be solved.
• Space Complexity: O(N*2) + O(N), As we are using a recursion stack space of O(N) and a 2D array O(N*2).

3️⃣ Tabulation

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

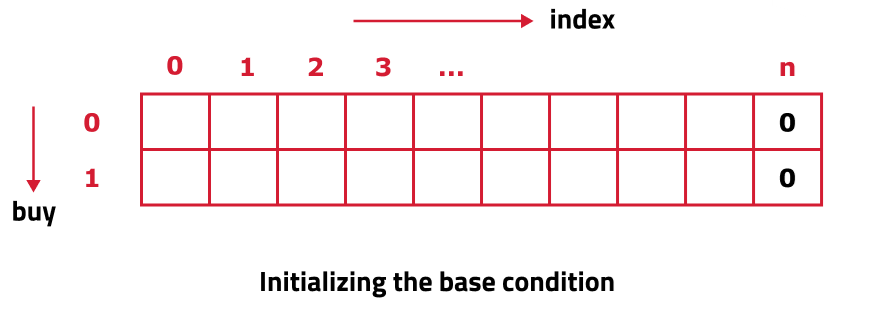
• Declare a dp array of size [n+1][2]: As there are two changing parameters in the recursive solution, 'ind' and 'buy'. The maximum value 'ind' can attain is (n) and including 0 its n+1, where n is the size of array and for 'buy' only two values possible 0, 1.
• Setting Base Cases in the Array: In the recursive code, our base condition was when If ind == n, it means we have finished trading on all days, and there is no more money that we can get, therefore simply return 0. As this is the last row, so set dp[n][0] = dp[n][1] = 0(the case when we had exhausted the number of days of the stock market).

• Iterative Computation Using Loops: Set two nested for loops, the outer loop (for variable ind) moves from n-1 to 0 and the inner loop (for variable buy) moves from 0 to 1. In every iteration, calculate the value according to the memoization logic.

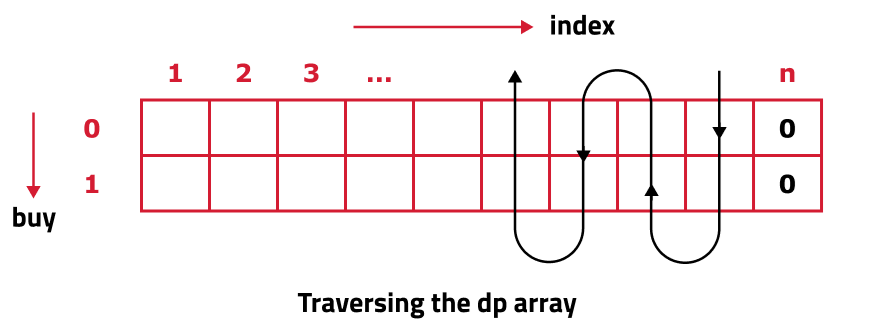
• Choosing the maximum: As we are looking to maximize the profit earned, return the maximum value in all the cases as discussed in memoization approach.
• Returning the answer: The element dp[0][0] of the dp array is returned because it holds the optimal solution to the entire problem after the computation has been completed.

Intuition:

• We create a table (dp) to iteratively compute the maximum profit for each day (index) and each state (holding or not holding`).
• The profit at any state (index, holding) depends only on the decisions we can take at that state:
  1. If not holding a stock:
     • Buy the stock, leading to the next state (index + 1, holding = 1).
     • Skip the transaction, staying in (index + 1, holding = 0).
  2. If holding a stock:
     • Sell the stock, leading to the next state (index + 1, holding = 0).
     • Hold the stock, staying in (index + 1, holding = 1).
• Use these transitions to compute the solution iteratively for all states.

Approach:

1. Define State Variables:
   • dp[i][0]: Maximum profit on day i if not holding a stock.
   • dp[i][1]: Maximum profit on day i if holding a stock.
2. Base Case:
   • On the last day (n - 1):
     • dp[n - 1][0] = 0: If not holding a stock, no profit can be made.
     • dp[n - 1][1] = -prices[n - 1]: If holding a stock, the maximum profit is the negative value of the stock price.
3. Transition:
   • If not holding a stock (dp[i][0]):
     • dp[i][0] = max(dp[i + 1][0], dp[i + 1][1] + prices[i])
       • Skip: dp[i + 1][0]
       • Sell: dp[i + 1][1] + prices[i]
   • If holding a stock (dp[i][1]):
     • dp[i][1] = max(dp[i + 1][1], dp[i + 1][0] - prices[i])
       • Hold: dp[i + 1][1]
       • Buy: dp[i + 1][0] - prices[i]
4. Iterate Backwards:
   • Start from the second-to-last day (n - 2) and compute dp[i][0] and dp[i][1] for all days.
5. Final Result:
   • The answer is dp[0][0], as we begin on day 0 without holding any stock.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    //Function to find maximum profit earned using tabulation
    int func(vector<int> &arr, int n) {
        // Create a DP table to memoize results
        vector<vector<int>> dp(n + 1, vector<int>(2, -1));

        // Base condition
        dp[n][0] = dp[n][1] = 0;

        int profit;

        // Loop through the array in reverse order
        for (int ind = n - 1; ind >= 0; ind--) {
            for (int buy = 0; buy <= 1; buy++) {
                // We can buy the stock
                if (buy == 0) { 
                    profit = max(0 + dp[ind + 1][0], (-1)*arr[ind] + dp[ind + 1][1]);
                }
            
                // We can sell the stock
                if (buy == 1) { 
                    profit = max(0 + dp[ind + 1][1], arr[ind] + dp[ind + 1][0]);
                }

                dp[ind][buy] = profit;
            }
        }

        /* The maximum profit is stored in
        dp[0][0] after all calculations*/
        return dp[0][0];
    }
public:
    //Function to calculate the maximum profit earned
    int stockBuySell(vector<int> &arr, int n){
        //Return the maximum profit
        return func(arr, n);
    }
};
int main() {
    int n = 6;
    vector<int> arr = {7, 1, 5, 3, 6, 4};
    
    //Create an instance of Solution class
    Solution sol;

    // Call the getMaximumProfit function and print the result
    cout << "The maximum profit that can be generated is " << sol.stockBuySell(arr, n);

    return 0;
}

OR:

 #include <vector>
#include <iostream>
using namespace std;

int maxProfit(vector<int>& prices) {
    int n = prices.size();
    if (n == 0) return 0;

    // dp[i][0] = max profit on day i if not holding a stock
    // dp[i][1] = max profit on day i if holding a stock
    vector<vector<int>> dp(n, vector<int>(2, 0));

    // Base cases for the last day
    dp[n - 1][0] = 0;               // Not holding a stock on the last day
    dp[n - 1][1] = -prices[n - 1];  // Holding a stock on the last day

    // Fill the dp table from the second-to-last day to the first day
    for (int i = n - 2; i >= 0; i--) {
        dp[i][0] = max(dp[i + 1][0], dp[i + 1][1] + prices[i]); // Max of skipping or selling
        dp[i][1] = max(dp[i + 1][1], dp[i + 1][0] - prices[i]); // Max of holding or buying
    }

    // The result is the maximum profit starting on day 0 without holding stock
    return dp[0][0];
}

int main() {
    vector<int> prices = {3, 2, 6, 5, 0, 3};
    cout << "Maximum Profit: " << maxProfit(prices) << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity: O(N*2), As, here are two nested loops that account for O(N*2) complexity.
• Space Complexity: O(N*2), As a 2D array of size N*2 is used

4️⃣ Space Optimized