Understanding the Problem

Post-order traversal is defined by the sequence in which nodes are visited. Starting from the left child, the algorithm visits the left subtree, then the right subtree, and finally the root node. This sequence ensures that a node's children are processed before the node itself, making it useful for tasks such as expression tree evaluation and memory management.

Consider the following binary tree:

    1
   / \
  2   3
 / \
4   5

The post-order traversal of this tree would be: 4, 5, 2, 3, 1.

Different Approach

1️⃣ Recursive Approach:

Intuition:

Post-order traversal is another method for exploring trees, where we follow the sequence of exploring the left subtree first, then the right subtree, and finally visiting the root node. This approach ensures that we only process the current node after we have fully traversed its left and right subtrees. The order we follow is Left, Right, and then Root.

Approach:

In post-order traversal, the method starts by fully exploring the left subtree, followed by the right subtree, and then processing the current node. This traversal method is particularly useful in scenarios where you need to ensure that both child nodes are processed before the parent node. We use a recursive approach to naturally follow this sequence, with each call diving deeper into the left and right children before handling the current node.

The recursive approach is straightforward. For a given node:

• Traverse the left subtree using a recursive call.
• Traverse the right subtree using a recursive call.
• Process the current node.

void postOrderRecursive(Node* root) {
    if (root == nullptr) {
        return;
    }

    postOrderRecursive(root->left);
    postOrderRecursive(root->right);
    cout << root->data << " ";
}

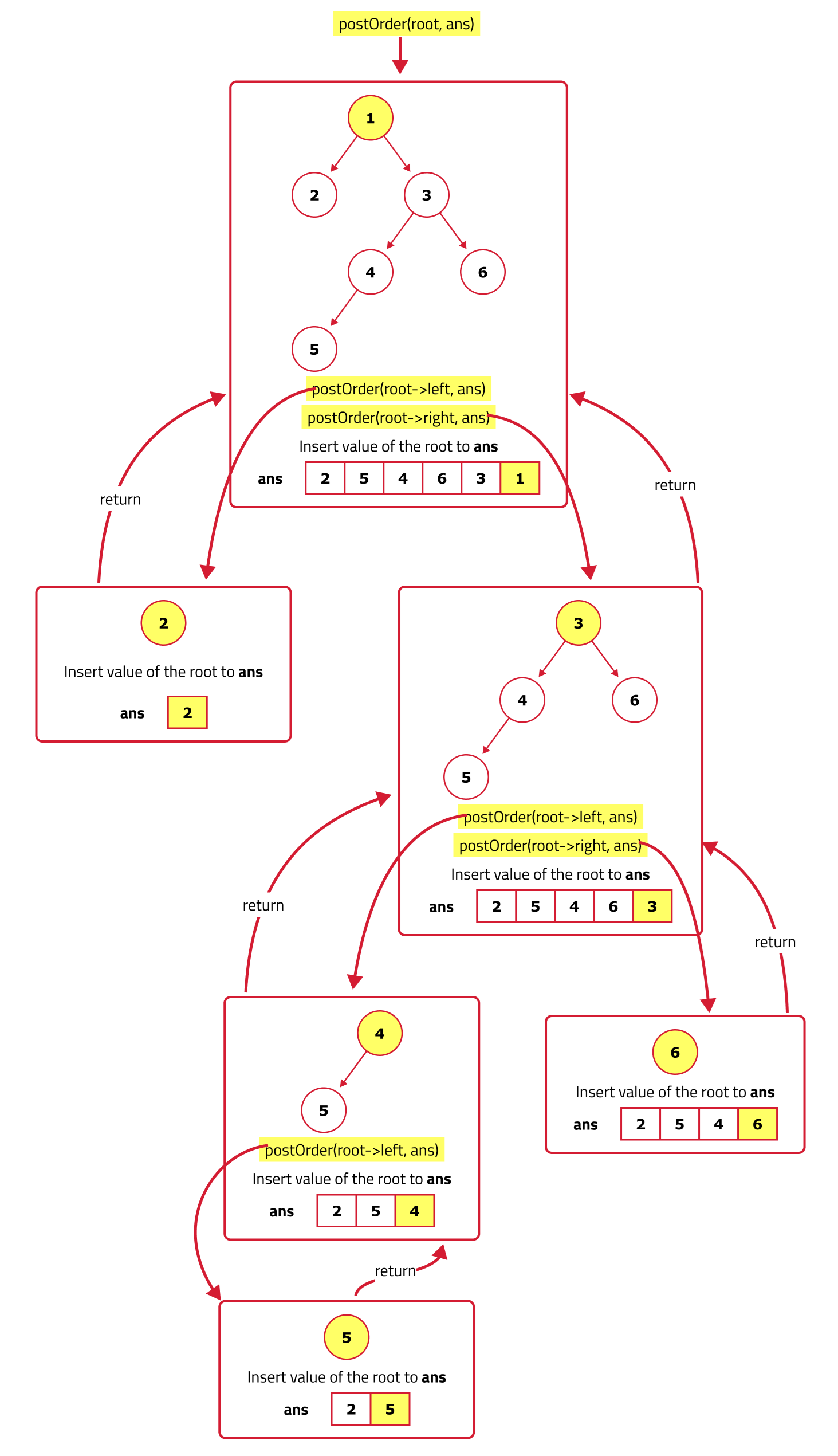
Dry Run:

Let's break down the steps and the data structures involved:

• Step 1: Check if the current node is null. If it is, we've reached the end of a subtree, and the recursive function stops.
• Step 2: Recursively traverse the left subtree. This means making a call to the postorder function on the left child of the current node.
• Step 3: Recursively traverse the right subtree by calling the postorder function on the right child of the current node.
• Step 4: Process the current node by adding its value to the postorder traversal array. This step is done after the left and right subtrees have been fully explored.

This recursive approach uses the call stack to manage the traversal, ensuring that each node is visited in the correct post-order sequence.

Code:

#include <bits/stdc++.h>
using namespace std;

// TreeNode structure for the binary tree
struct TreeNode {
    int data;
    TreeNode* left;
    TreeNode* right;
    // Constructor to initialize
    // the TreeNode with a value
    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
    
class Solution{
    private:
    // Function to perform postorder
    // traversal recursively
    void recursivePostorder(TreeNode* root, vector<int>& arr){
        // Base case: if root is null, return
        if(root==NULL){
            return;
        }
        // Traverse left subtree
        recursivePostorder(root->left, arr);
        // Traverse right subtree
        recursivePostorder(root->right, arr);
        // Visit the TreeNode
        // (append TreeNode's data to the array)
        arr.push_back(root->data);
    }
    public:
    // Function to get the postorder
    // traversal of a binary tree
    vector<int> postorder(TreeNode* root){
        // Create a vector to
        // store the traversal result
        vector<int> arr;
        // Perform postorder traversal
        // starting from the root
        recursivePostorder(root, arr);
        // Return the postorder
        // traversal result
        return arr;
    }
};

// Function to print the
// elements of a vector
void printVector(const vector<int>& vec) {
    // Iterate through the vector
    // and print each element
    for (int num : vec) {
        cout << num << " ";
    }
    cout << endl;
}

// Main function
int main()
{
    // Creating a sample binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    
    Solution sol = Solution();
    // Getting postorder traversal
    vector<int> result = sol.postorder(root);

    // Printing the postorder
    // traversal result
    cout << "Postorder traversal: ";
    printVector(result);

    return 0;
}

Complexity Analysis:

• Time Complexity: O(n), where n is the number of nodes in the tree.
• Space Complexity: O(h), where h is the height of the tree (recursion call stack).

2️⃣ Iterative Approach using Stack:

An iterative approach often uses a stack to simulate the function call stack in recursion.

• Push the root node onto the stack.
• While the stack is not empty:
  → Pop a node from the stack.
  → Push the node's left and right child onto the stack.
  → Process the node.

void postOrderIterative(Node* root) {
    stack<Node*> s;
    stack<Node*> output;

    s.push(root);

    while (!s.empty()) {
        Node* current = s.top();
        s.pop();
        output.push(current);

        if (current->left) {
            s.push(current->left);
        }
        if (current->right) {
            s.push(current->right);
        }
    }

    while (!output.empty()) {
        cout << output.top()->data << " ";
        output.pop();
    }
}

Code:

#include <iostream>
#include <stack>
using namespace std;

struct Node {
    int data;
    Node* left;
    Node* right;

    Node(int value) : data(value), left(nullptr), right(nullptr) {}
};

// Iterative Algorithm
void postOrderIterative(Node* root) {
    stack<Node*> s;
    stack<Node*> output;

    s.push(root);

    while (!s.empty()) {
        Node* current = s.top();
        s.pop();
        output.push(current);

        if (current->left) {
            s.push(current->left);
        }
        if (current->right) {
            s.push(current->right);
        }
    }

    while (!output.empty()) {
        cout << output.top()->data << " ";
        output.pop();
    }
}

int main() {
    // Constructing a sample binary tree
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);

    cout << "Iterative Post-Order Traversal: ";
    postOrderIterative(root);
    cout << endl;

    return 0;
}

// Output
Iterative Post-Order Traversal: 4 5 2 3 1 

Complexity Analysis:

• Time Complexity: O(n)
• Space Complexity: O(h), where h is the height of the tree (maximum nodes in the stack at any given time).