The knapsack problem is a classic optimization problem in computer science where given a set of items, each with a weight and a value, and a knapsack with a maximum weight capacity, the goal is to maximize the total value of items that can be included in the knapsack without exceeding its capacity.
Variations of Knapsack Problem
- 0/1 Knapsack Problem:
- In this variation, items can either be included or excluded from the knapsack. You cannot take fractions of items.
- Objective: Maximize the total value of items without exceeding the knapsack's weight capacity.
- Fractional Knapsack Problem:
- In this variation, items can be included in fractions. You can take fractions of items according to their weight.
- Objective: Maximize the total value of items without exceeding the knapsack's weight capacity.
- Unbounded Knapsack Problem:
- In this variation, there is an unlimited supply of each item. You can take as many instances of each item as you want.
- Objective: Maximize the total value of items without exceeding the knapsack's weight capacity.
- Multiple Knapsack Problem:
- In this variation, there are multiple knapsacks, each with it own capacity. You need to distribute the items among the knapsacks to maximize the total value.
- Objective: Maximize the total value of items while respecting the capacity constraints of each knapsack.
- Bounded Knapsack Problem:
- In this variation, there is a limited number of instances for each item. You cannot take more instances of an item than its given limit.
- Objective: Maximize the total value of items without exceeding the knapsack's weight capacity and respecting the limits on the number of instances for each item.
0 and 1 Knapsack
Problem Statement
Given two integer arrays, val and wt, each of size N, which represent the values and weights of N items respectively, and an integer W representing the maximum capacity of a knapsack, determine the maximum value achievable by selecting a subset of the items such that the total weight of the selected items does not exceed the knapsack capacity W.
Each item can either be picked in its entirety or not picked at all (0-1 property). The goal is to maximize the sum of the values of the selected items while keeping the total weight within the knapsack's capacity.
Example:
Example 1:
Input:
N = 4
val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
Output: 220
Explanation:
We have 3 items:
Item 1: Value = 60, Weight = 10
Item 2: Value = 100, Weight = 20
Item 3: Value = 120, Weight = 30
The knapsack capacity W = 50
Optimal Selection:
Pick Item 2 (Value = 100, Weight = 20)
Pick Item 3 (Value = 120, Weight = 30)
Total Weight: 20 + 30 = 50
Maximum Value = 100 + 120 = 220Example 2:
Input:
N = 3
val = [10, 20, 30]
wt = [1, 2, 3]
W = 5
Output: 50
Explanation:
We have 3 items:
Item 1: Value = 10, Weight = 1
Item 2: Value = 20, Weight = 2
Item 3: Value = 30, Weight = 3
The knapsack capacity W = 5
Optimal Solution:
Pick Item 2 (Value = 20, Weight = 2)
Pick Item 3 (Value = 30, Weight = 3)
Total Weight = 2 + 3 = 5
Maximum Value = 20 + 30 = 50Different Approaches
1️⃣ Recursive Approach
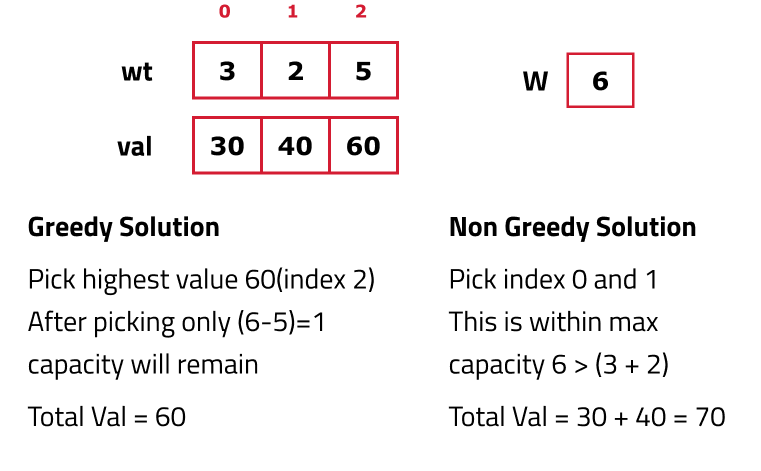
Why a Greedy Solution will not work:
As the question is asking for maximum value, the first approach that comes to our mind is greedy. A greedy solution will fail in this problem because there is no ‘uniformity’ in data. While selecting a local better choice we may choose an item that will in long term give less value. So we will solve this problem using recursion.
Steps to form the recursive solution:
- Express the problem in terms of indexes: We are given ‘n’ items. Their weight is represented by the ‘wt’ array and value by the ‘val’ array. So clearly one parameter will be ‘ind’, i.e index up to which the array items are being considered. There is one more parameter 'W', the capacity of the knapsack to decide whether we can pick an array item or not in the knapsack.
- So initially, we need to find f(n-1, W) where W is the overall capacity given to us. f(n-1, W) gives the maximum value of items that we can get from index 0 to n-1 with capacity W of the knapsack.
- Try out all possible choices at a given index: We need to generate all the subsequences. We will use the pick/non-pick technique. There will be two choices:
- Exclude the current element from the subsequence: First try to find a subsequence without considering the current index item. If we exclude the current item, the capacity of the bag will not be affected and the value added will be 0 for the current item. So we will call the recursive function f(ind-1,W),
- Include the current element in the subsequence: Try to find a subsequence by considering the current item to the knapsack. As we have included the item, the capacity of the knapsack will be updated to (W-wt[ind]) and the current item’s value (val[ind] will also be added to the further recursive call answer. We will make a recursive call to f(ind-1, W- wt[ind]).
Note: We will consider the current item in the subsequence only when the current element’s weight is less than or equal to the capacity ‘W’ of the knapsack, if it isn’t we will not be considering it.
f(ind, W){
notTake = 0 + f(ind-1, W)
take = INT_MIN
if(wt[ind] <= W)
take = val[ind] + f(ind-1, W-wt[ind])
}- Return the maximum of take and notTake: As we have to return the maximum amount of value, we will return the maximum of take and notTake as our answer.
f(ind, W){
notTake = 0 + f(ind-1, W)
take = INT_MIN
if(wt[ind] <= W)
take = val[ind] + f(ind-1, W-wt[ind])
return max(take, notTake)
}- Base Case:
- If ind==0, it means we are at the first item, so in that case we will check whether this item’s weight is less than or equal to the current capacity W, if it is, we simply return its value (val[0]) else we return 0.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/* Recursive function to solve 0-1 Knapsack problem.
Parameters:
- `wt`: Array of weights of the items.
- `val`: Array of values of the items.
- `n`: Total number of items.
- `index`: Current index in the items list.
- `remainingCapacity`: Remaining capacity of the knapsack.
Returns:
- The maximum value achievable with the given constraints.
*/
int knapsackRecursive(vector<int>& wt, vector<int>& val, int n, int index, int remainingCapacity) {
// Base case: If we have considered all items or if the remaining capacity is 0.
if (index >= n || remainingCapacity == 0) {
return 0;
}
// Option 1: Exclude the current item (move to the next item).
int excludeItem = knapsackRecursive(wt, val, n, index + 1, remainingCapacity);
// Option 2: Include the current item (if the weight of the item is less than or equal to the remaining capacity).
int includeItem = INT_MIN;
if (wt[index] <= remainingCapacity) {
includeItem = val[index] + knapsackRecursive(wt, val, n, index + 1, remainingCapacity - wt[index]);
}
// Return the maximum of including or excluding the current item.
return max(includeItem, excludeItem);
}
/* Function to solve the 0-1 Knapsack problem using the recursive approach.
Parameters:
- `wt`: Array of weights of the items.
- `val`: Array of values of the items.
- `n`: Total number of items.
- `W`: The maximum capacity of the knapsack.
Returns:
- The maximum value that can be obtained by selecting items without exceeding the knapsack capacity.
*/
int knapsack01(vector<int>& wt, vector<int>& val, int n, int W) {
return knapsackRecursive(wt, val, n, 0, W);
}
};
int main() {
// Example usage
Solution sol;
vector<int> weights = {2, 3, 4, 5}; // Weights of items
vector<int> values = {3, 4, 5, 6}; // Corresponding values of items
int n = weights.size(); // Total number of items
int capacity = 5; // Maximum weight capacity of the knapsack
// Call the knapsack function and print the result
cout << "Maximum value in Knapsack: " << sol.knapsack01(weights, values, n, capacity) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(2 ^ n), wherenis the size of the array. - Space Complexity:
O(n)
2️⃣ Memoization
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
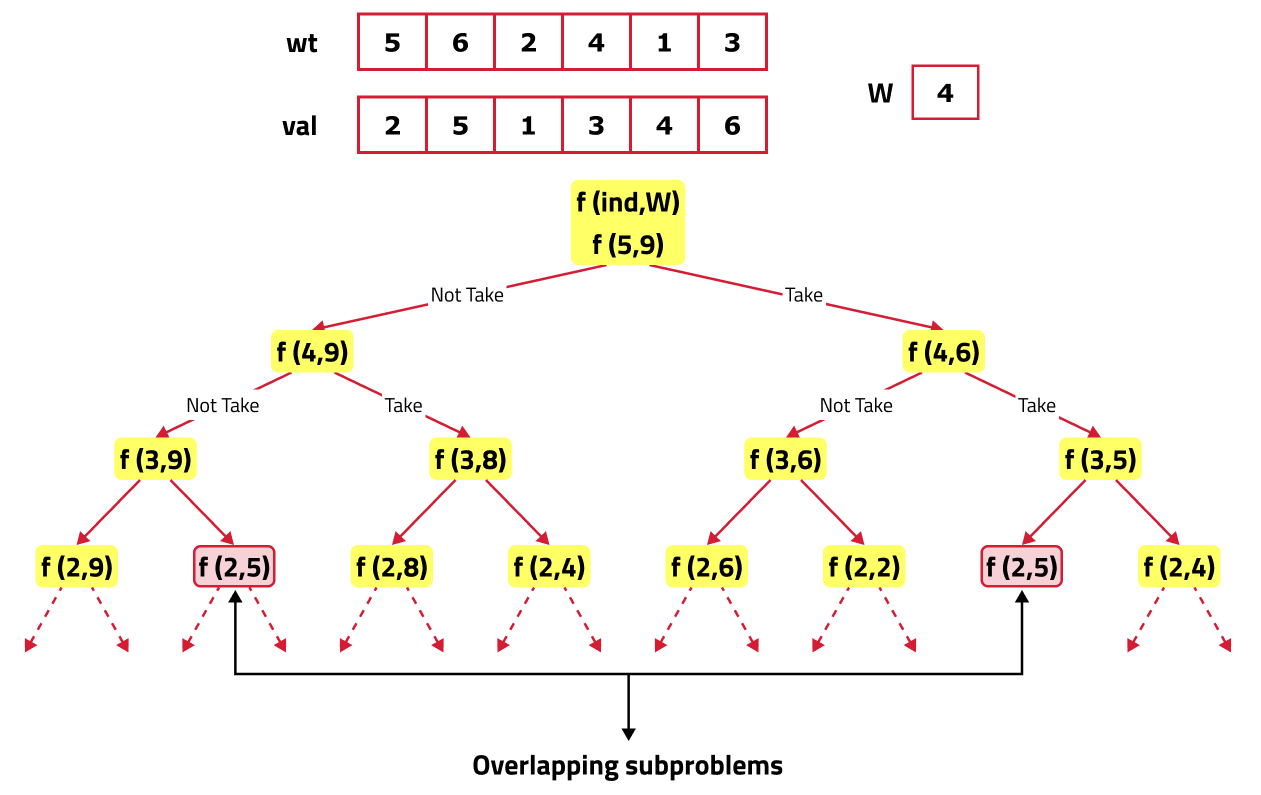
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][W+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The size of the input array is ‘N’, so the index will always lie between ‘0’ and ‘n-1’. The capacity can take any value between ‘0’ and ‘W’. Therefore 2D dp array(dp[n][W+1]) is needed.
- The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/*
This function uses recursion with memoization (top-down approach) to solve the 0-1 Knapsack problem.
Parameters:
- `wt`: Array of weights of the items.
- `val`: Array of values of the items.
- `n`: Total number of items.
- `index`: Current index in the item list being considered.
- `remainingCapacity`: Remaining capacity of the knapsack.
- `dp`: Memoization table to store the results of subproblems.
Returns:
- The maximum value achievable with the given constraints.
*/
int knapsackRecursive(vector<int>& wt, vector<int>& val, int n, int index, int remainingCapacity, vector<vector<int>>& dp) {
// Base case: if we have considered all items (index >= n).
if (index >= n) {
return 0;
}
// If this subproblem has already been solved, return the stored result.
if (dp[index][remainingCapacity] != -1) {
return dp[index][remainingCapacity];
}
// Option 1: Exclude the current item and move to the next item.
int excludeItem = knapsackRecursive(wt, val, n, index + 1, remainingCapacity, dp);
// Option 2: Include the current item (if its weight is less than or equal to the remaining capacity).
int includeItem = INT_MIN; // Initialize to a very small value.
if (wt[index] <= remainingCapacity) {
// If we can include this item, reduce the remaining capacity and add the item's value.
includeItem = val[index] + knapsackRecursive(wt, val, n, index + 1, remainingCapacity - wt[index], dp);
}
// Store the maximum value of either including or excluding the current item.
return dp[index][remainingCapacity] = max(includeItem, excludeItem);
}
/*
This function initializes the memoization table and calls the recursive function.
Parameters:
- `wt`: Array of weights of the items.
- `val`: Array of values of the items.
- `n`: Total number of items.
- `W`: Maximum weight capacity of the knapsack.
Returns:
- The maximum value that can be obtained by selecting items without exceeding the knapsack's weight capacity.
*/
int knapsack01(vector<int>& wt, vector<int>& val, int n, int W) {
// Initialize a 2D memoization table with -1, indicating that no subproblem has been solved yet.
vector<vector<int>> dp(n, vector<int>(W + 1, -1));
// Start the recursive process from the first item (index 0) and the full knapsack capacity W.
return knapsackRecursive(wt, val, n, 0, W, dp);
}
};
int main() {
// Example usage of the knapsack problem.
Solution sol;
// Example weights and values of items.
vector<int> weights = {2, 3, 4, 5}; // Weights of the items
vector<int> values = {3, 4, 5, 6}; // Corresponding values of the items
// Total number of items
int n = weights.size();
// Knapsack's maximum weight capacity
int capacity = 5;
// Call the knapsack01 function and print the maximum value achievable.
cout << "Maximum value in Knapsack: " << sol.knapsack01(weights, values, n, capacity) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(n * W) - Space Complexity:
O(n * W)
Let's illustrate the problem with a simple example:
Suppose you have a knapsack with a weight capacity of 10 units and the following items:
| Item | Weight | Value |
|---|---|---|
| A | 2 | 6 |
| B | 3 | 5 |
| C | 5 | 10 |
| D | 7 | 12 |
The goal is to select items to maximize the total value while ensuring that the total weight does not exceed 10.
Solution (0/1) Knapsack Problem
#include <iostream>
#include <vector>
using namespace std;
int knapsack(int W, vector<int>& wt, vector<int>& val, int n) {
vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));
for (int i = 1; i <= n; ++i) {
for (int w = 1; w <= W; ++w) {
if (wt[i - 1] <= w) {
dp[i][w] = max(val[i - 1] + dp[i - 1][w - wt[i - 1]], dp[i - 1][w]);
} else {
dp[i][w] = dp[i - 1][w];
}
}
}
return dp[n][W];
}
int main() {
vector<int> wt = {2, 3, 5, 7};
vector<int> val = {6, 5, 10, 12};
int W = 10;
int n = wt.size();
cout << "Maximum value that can be obtained: " << knapsack(W, wt, val, n) << endl;
return 0;
}
Unbounded Knapsack
Problem Statement
Given two integer arrays, val and wt, each of size N, representing the values and weights of N items respectively, and an integer W, representing the maximum capacity of a knapsack, determine the maximum value achievable by selecting a subset of the items such that the total weight of the selected items does not exceed the knapsack capacity W. The goal is to maximize the sum of the values of the selected items while keeping the total weight within the knapsack's capacity.
An infinite supply of each item can be assumed.
Examples
Example 1:
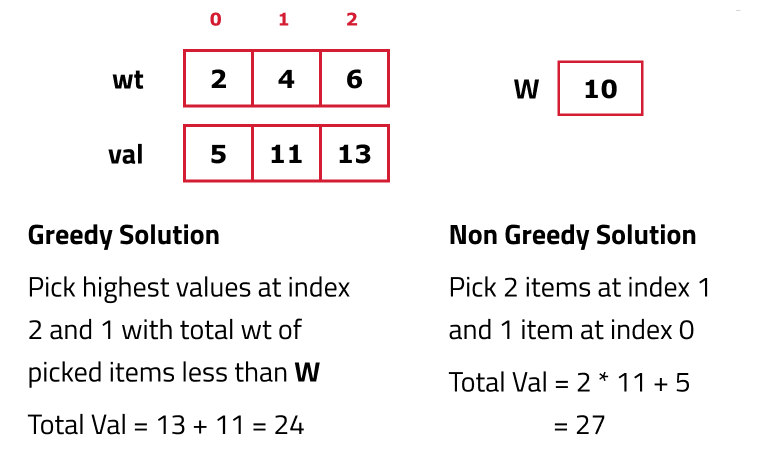
Input: val = [5, 11, 13], wt = [2, 4, 6], W = 10
Output: 27
Explanation: Select 2 items with weights 4 and 1 item with weight 2 for a total value of 11+11+5 = 27.Example 2:
Input: val = [10, 40, 50, 70], wt = [1, 3, 4, 5], W = 8
Output: 110
Explanation: Select items with weights 3 and 5 for a total value of 40 + 70 = 110.Different Approaches
1️⃣ Recursive Approach
Why a Greedy Solution will not work:
The first approach that comes to our mind is greedy. A greedy solution will fail in this problem because there is no ‘uniformity’ in data. While selecting a local better choice we may choose an item that will in long term give less value.
As the greedy approach doesn’t work, we will try to generate all possible combinations using recursion and select the combination which gives us the maximum value in the given constraints.
Steps to form the recursive solution:
- Express the problem in terms of indexes: We are given ‘n’ items. Their weight is represented by the ‘wt’ array and value by the ‘val’ array. So clearly one parameter will be ‘ind’, i.e index upto which the array items are being considered. There is one more parameter “W”, to keep track of the capacity of the knapsack to decide whether we can pick an array item or not.
- So, initially we need to find f(n-1, W) where W is the overall capacity given to us. f(n-1, W) gives the maximize the sum of the values of the selected items from index 0 to n-1 with capacity W of the knapsack.
- Try out all possible choices at a given index: We need to generate all the subsequences. So, use the pick/non-pick technique. There are two choices for every index:
- Exclude the current element from the knapsack: First try to find a solution without considering the current index item. If we exclude the current item, the capacity of the bag will not be affected and the value added will be 0 for the current item. So call the recursive function f(ind-1,W).
- Include the current element in the knapsack: Try to find a solution by considering the current item to the knapsack. As we have included the item, the capacity of the knapsack will be updated to W-wt[ind] and the current item’s value (val[ind]) will also be added to the further recursive call answer.
Now here is the catch, as there is an unlimited supply of coins, we want to again form a solution with the same item value. So we will not recursively call for f(ind-1, W-wt[ind]) rather stay at that index only and call for f(ind, W-wt[ind]) to find the answer.
Note: Consider the current item in the knapsack only when the current element’s weight is less than or equal to the capacity ‘W’ of the knapsack, if it isn’t do not consider it.
f(ind, W){
notTake = 0 + f(ind-1, W)
take = INT_MIN
if(wt[ind] <= W)
take = val + f(ind, W-wt[ind])
}- Return the maximum of 'take' and 'notTake': As we have to return the maximum amount of value, return the max of take and notTake as our answer.
f(ind, W){
notTake = 0 + f(ind-1, W)
take = INT_MIN
if(wt[ind] <= W)
take = val + f(ind, W-wt[ind])
return max(notTake, take)
}- Base Cases: If ind==0, it means we are at the first item. Now, in an unbounded knapsack we can pick an item any number of times. As there is only one item left, pick for W/wt[0] times because ultimately we want to maximize the value of items while respecting the constraint of weight of the knapsack. The value added will be the product of the number of items picked and value of the individual item. Therefore return (W/wt[0]) * val[0].
Code:
class Solution {
public:
// Recursive function to solve the Unbounded Knapsack problem
int maximizeValue(vector<int>& weights, vector<int>& values, int totalItems, int currentIndex, int remainingCapacity) {
// Base Case 1: If the remaining capacity is 0, no more value can be added
if (remainingCapacity == 0) {
return 0;
}
// Base Case 2: If we have considered all items, stop the recursion
if (currentIndex >= totalItems) {
return 0;
}
// Case 1: Include the current item (only if its weight is within the remaining capacity)
int includeValue = 0;
if (weights[currentIndex] <= remainingCapacity) {
includeValue = values[currentIndex] +
maximizeValue(weights, values, totalItems, currentIndex, remainingCapacity - weights[currentIndex]);
}
// Case 2: Exclude the current item and move to the next item
int excludeValue = maximizeValue(weights, values, totalItems, currentIndex + 1, remainingCapacity);
// Return the maximum of the two cases
return max(includeValue, excludeValue);
}
// Public function to initiate the recursive process for Unbounded Knapsack
int unboundedKnapsack(vector<int>& weights, vector<int>& values, int totalItems, int capacity) {
return maximizeValue(weights, values, totalItems, 0, capacity);
}
};
Complexity Analysis:
- Time Complexity:
O(2 ^ N), As each element has two choices and there are total N elements to be considered. - Space Complexity:
O(N), As the maximum depth of the recursion stack can go up to N.
2️⃣ Memoization
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
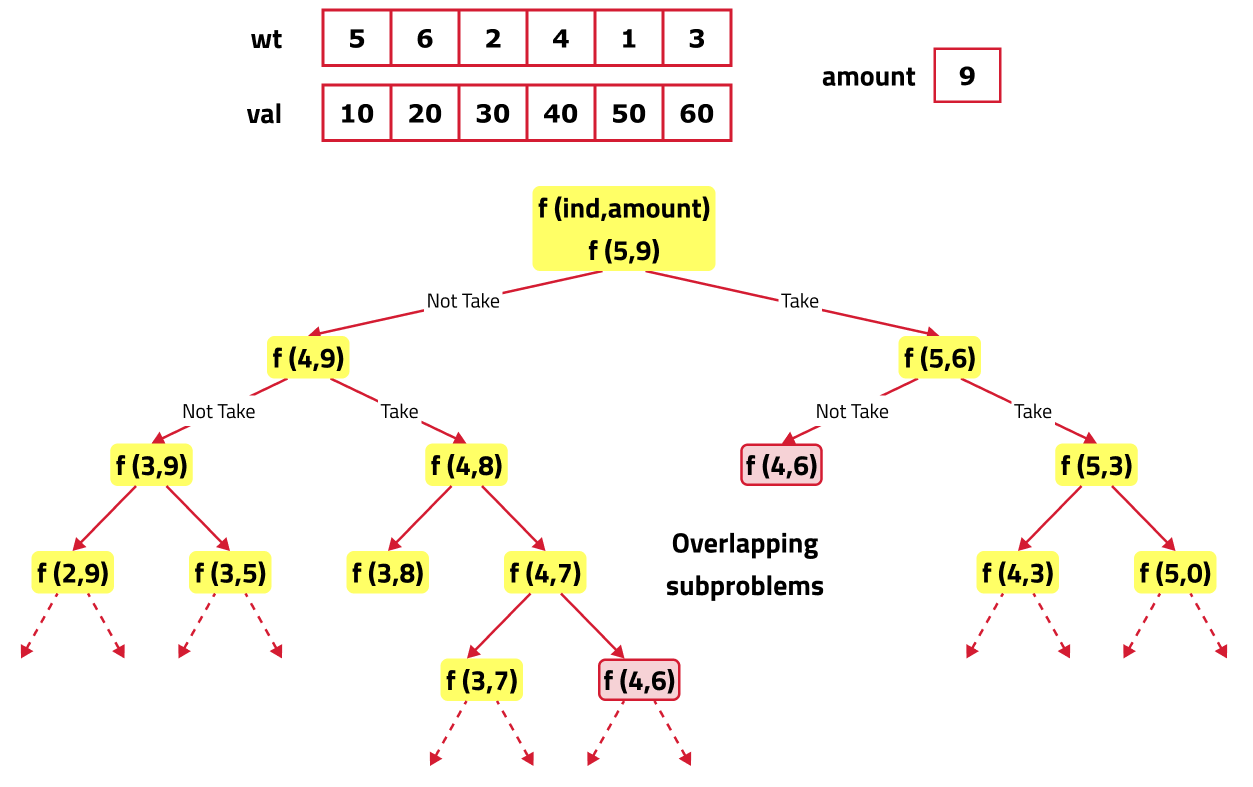
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][W+1]: As there are two changing parameters in the recursive solution, 'ind' and 'W'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'W', which denotes weight of the knapsack, only values between 0 to W. Therefore, we need 2D dp array.
- The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
class Solution {
public:
// Recursive function with memoization to solve the Unbounded Knapsack problem
int maximizeValue(vector<int>& weights, vector<int>& values, int totalItems, int currentIndex, int remainingCapacity, vector<vector<int>>& memo) {
// Base Case 1: If the remaining capacity is 0, no more value can be added
if (remainingCapacity == 0) {
return 0;
}
// Base Case 2: If we have considered all items, stop the recursion
if (currentIndex >= totalItems) {
return 0;
}
// Check if the result is already computed
if (memo[currentIndex][remainingCapacity] != -1) {
return memo[currentIndex][remainingCapacity];
}
// Case 1: Include the current item (only if its weight is within the remaining capacity)
int includeValue = 0;
if (weights[currentIndex] <= remainingCapacity) {
includeValue = values[currentIndex] +
maximizeValue(weights, values, totalItems, currentIndex, remainingCapacity - weights[currentIndex], memo);
}
// Case 2: Exclude the current item and move to the next item
int excludeValue = maximizeValue(weights, values, totalItems, currentIndex + 1, remainingCapacity, memo);
// Store the result in the memo table and return
return memo[currentIndex][remainingCapacity] = max(includeValue, excludeValue);
}
// Public function to initiate the recursive process for Unbounded Knapsack
int unboundedKnapsack(vector<int>& weights, vector<int>& values, int totalItems, int capacity) {
vector<vector<int>> memo(totalItems, vector<int>(capacity + 1, -1));
return maximizeValue(weights, values, totalItems, 0, capacity, memo);
}
};
Complexity Analysis:
- Time Complexity:
O(N*W), as there are N*W states therefore at max ‘N*W’ new problems will be solved. - Space Complexity:
O(N*W) + O(N), the stack space will be O(N) and a 2D array of size N*W is used.