Problem Statement
Given two strings str1 and str2, find the length of their longest common subsequence.
A subsequence is a sequence that appears in the same relative order but not necessarily contiguous and a common subsequence of two strings is a subsequence that is common to both strings.
LeetCode:
Constraints:
1 <= text1.length, text2.length <= 1000
text1 and text2 consist of only lowercase English characters.1 ≤ str1.length, str2.length ≤ 1000- It tells you the maximum size your algorithm must handle. Since 1000*1000 = 1,000,000, a DP solution with
O(n*m)time andO(m)space is acceptable and efficient.
- It tells you the maximum size your algorithm must handle. Since 1000*1000 = 1,000,000, a DP solution with
Examples
Example 1:
Input: str1 = "bdefg", str2 = "bfg"
Output: 3
Explanation: The longest common subsequence is "bfg", which has a length of 3.Example 2:
Input: str = "mnop", str2 = "mnq"
Output: 2
Explanation: The longest common subsequence is "mn", which has a length of 2.Different Approaches
1️⃣ Recursive Approach
We are given two strings, S1, and S2 (suppose of same length n), the simplest approach will be to generate all the subsequences and store them, then manually find out the longest common subsequence.
We would want to try something that can give us the longest common subsequence on the way of generating all subsequences. To generate all subsequences we will use recursion and in the recursive logic we will figure out a way to solve this problem.
Steps to form the recursive solution:
- Express the problem in terms of indexes: We are given two strings S1 and S2. A single variable can’t express both the strings at the same time, so we will use two variables 'ind1' and 'ind2'. They mean that we are considering string S1 from index 0 to 'ind1' and string S2 from index 0 to 'ind2'. So f(ind1, ind2) will give the longest common subsequence in S1 and S2.

- Explore all possibilities at a given index: In the function f(ind1,ind2), ind1 and ind2 are representing two characters from strings S1 and S2 respectively. For example: Now, there can be two possibilities,
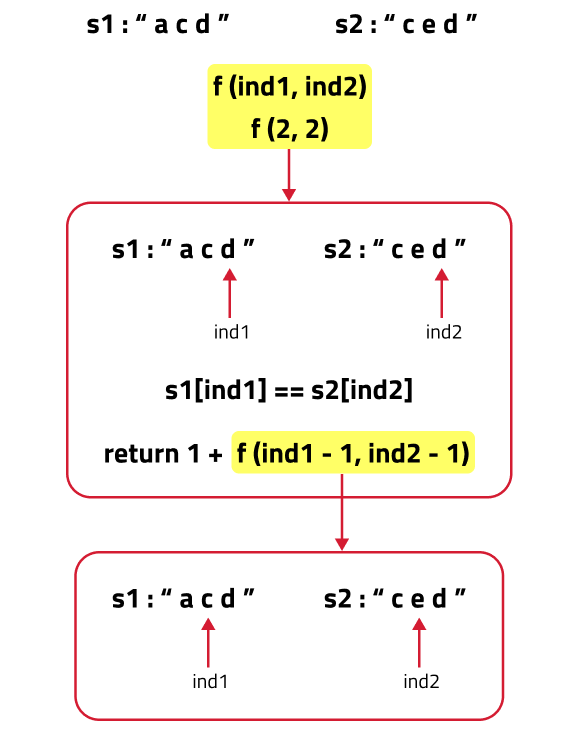
If (S1[ind1] == S2[ind2]) as in the figure below. In this case this common element will represent a unit length common subsequence, so we can say that we have found one character and we can shrink both the strings by 1 to find the longest common subsequence in the remaining pair of strings.
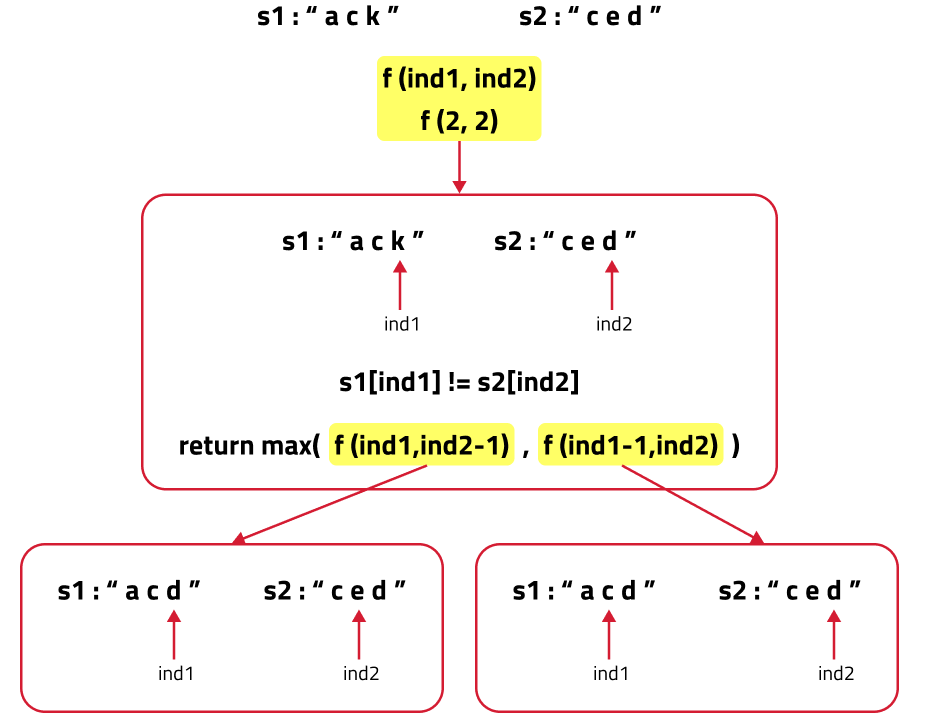
- If (S1[ind1] != S2[ind2]) as in the figure given below. In this case we know that the current characters represented by ind1 and ind 2 will be different. So, we need to compare the ind1 character with shrunk S2 and ind2 with shrunk S1. But how do we make this comparison ? If we make a single recursive call as we did above to f(ind1-1,ind2-1), we may lose some characters of the subsequence. Therefore we make two recursive calls: one to f(ind1,ind2-1) (shrinking only S1) and one to f(ind1-1,ind2) (shrinking only S2). Then when we return max of both the calls.
- Return the maximum of the choices: In the first case, we have only one choice but in the second case we have two choices, as we have to return the longest common subsequences, we will return the maximum of both the choices in the second case.
/*It is pseudocode and it is not tied to
any specific programming language.*/
f(ind1, ind2){
if(s1[ind1] == s2[ind2])
return 1 + f(ind1 - 1, ind2 - 1)
else
return 0 + max(f(ind1, ind2-1), f(ind1 - 1, ind2))
}- Base Case: For a case like this

As S1[ind1] != S2[ind2], we will make a call to f(0-1,1), i.e f(-1,1) but a negative index simply means that there are no more indexes to be explored, so we simply return 0. Same is the case when S1[ind1]==S2[ind2]. So, when any of the index (ind1, ind2) becomes negative we will return 0.
Code:
Starting from 0:
class Solution {
public:
// Recursive function to find the LCS
int recursive(string& str1, string& str2, int index1, int index2) {
// Base case: If either string is fully traversed
if (index1 >= str1.size() || index2 >= str2.size()) {
return 0;
}
// Case 1: If characters match, move both indices
if (str1[index1] == str2[index2]) {
return 1 + recursive(str1, str2, index1 + 1, index2 + 1);
}
// Case 2: If characters don't match, try skipping one character from either string
int skipStr1 = recursive(str1, str2, index1 + 1, index2); // Skip character from str1
int skipStr2 = recursive(str1, str2, index1, index2 + 1); // Skip character from str2
// Return the maximum of the two options
return max(skipStr1, skipStr2);
}
// Public function to calculate LCS using recursion
int lcs(string str1, string str2) {
return recursive(str1, str2, 0, 0);
}
};Starting from end:
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Function to find the length of the
Longest Common Subsequence (LCS)*/
int func(string& s1, string& s2, int ind1, int ind2) {
// Base case
if (ind1 < 0 || ind2 < 0)
return 0;
/* If the characters at the current
indices match, increment the LCS length*/
if (s1[ind1] == s2[ind2])
return 1 + func(s1, s2, ind1 - 1, ind2 - 1);
else
return max(func(s1, s2, ind1, ind2 - 1), func(s1, s2, ind1 - 1, ind2));
}
public:
/* Function to calculate the length
of the Longest Common Subsequence*/
int lcs(string str1, string str2) {
int n = str1.size();
int m = str2.size();
//Return the result
return func(str1, str2, n - 1, m - 1);
}
};
int main() {
string s1 = "acd";
string s2 = "ced";
//Create an instance of Solution class
Solution sol;
// Call the function to find and output
cout << "The Length of Longest Common Subsequence is " << sol.lcs(s1, s2) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(2 ^ min(m + n)), wheremandnare the lengths ofstr1andstr2. - Space Complexity:
O(n + m)- As we are using a recursion stack space.
2️⃣ Memoization
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
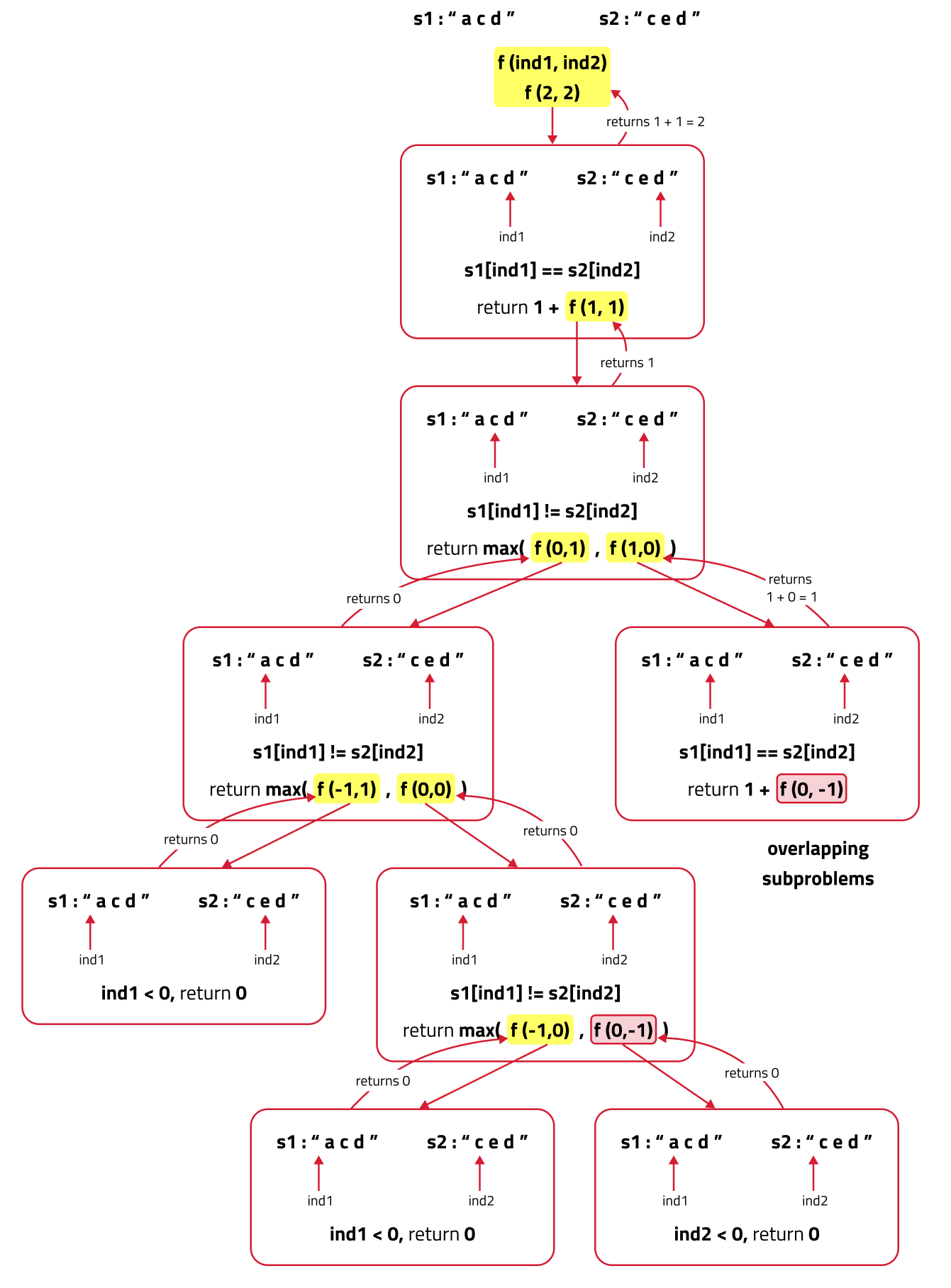
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][m]: where n and m are the lengths of S1 and S2 respectively. As there are two changing parameters in the recursive solution, 'ind1' and 'ind2'. The maximum value 'ind1' can attain is (n) and 'ind2' can attain maximum value of (m). Therefore, we need 2D dp array.
- The dp array shows the calculations of the subproblems, initialize it with -1 to show that no subproblem is solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
Starting from 0:
class Solution {
public:
int recursiveMemo(string& str1, string& str2, int index1, int index2, vector<vector<int>>& dp) {
// Base case: If either string is fully traversed
if (index1 >= str1.size() || index2 >= str2.size()) {
return 0;
}
// If result is already computed, return it
if (dp[index1][index2] != -1) {
return dp[index1][index2];
}
// Case 1: If characters match
if (str1[index1] == str2[index2]) {
dp[index1][index2] = 1 + recursiveMemo(str1, str2, index1 + 1, index2 + 1, dp);
} else {
// Case 2: If characters don't match
int skipStr1 = recursiveMemo(str1, str2, index1 + 1, index2, dp);
int skipStr2 = recursiveMemo(str1, str2, index1, index2 + 1, dp);
dp[index1][index2] = max(skipStr1, skipStr2);
}
return dp[index1][index2];
}
int lcs(string str1, string str2) {
int m = str1.size(), n = str2.size();
vector<vector<int>> dp(m, vector<int>(n, -1)); // Initialize memoization table
return recursiveMemo(str1, str2, 0, 0, dp);
}
};Starting from end:
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Function to find the length of the
Longest Common Subsequence (LCS)*/
int func(string& s1, string& s2, int ind1, int ind2, vector<vector<int>>& dp) {
// Base case
if (ind1 < 0 || ind2 < 0)
return 0;
/* If the result for this pair of indices
is already calculated, return it*/
if (dp[ind1][ind2] != -1)
return dp[ind1][ind2];
/* If the characters at the current
indices match, increment the LCS length*/
if (s1[ind1] == s2[ind2])
return dp[ind1][ind2] = 1 + func(s1, s2, ind1 - 1, ind2 - 1, dp);
else
return dp[ind1][ind2] = max(func(s1, s2, ind1, ind2 - 1, dp), func(s1, s2, ind1 - 1, ind2, dp));
}
public:
/* Function to calculate the length
of the Longest Common Subsequence*/
int lcs(string str1, string str2) {
int n = str1.size();
int m = str2.size();
vector<vector<int>> dp(n, vector<int>(m, -1));
//Return the result
return func(str1, str2, n - 1, m - 1, dp);
}
};
int main() {
string s1 = "acd";
string s2 = "ced";
//Create an instance of Solution class
Solution sol;
// Call the function to find and output
cout << "The Length of Longest Common Subsequence is " << sol.lcs(s1, s2) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(n*m), wherenandmis the length of thestr1andstr2. - Space Complexity:
O(N*M) + O(N+M), We are using an auxiliary recursion stack space(O(N+M)) and a 2D array (O(N*M)).
3️⃣ Tabulation
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n + 1][m + 1]: where n and m are the lengths of S1 and S2 respectively. As there are two changing parameters in the recursive solution, 'ind1' and 'ind2'. The maximum value 'ind1' can attain is (n) and 'ind2' can attain maximum value of (m). Therefore, we need 2D dp array.
- Setting Base Cases in the Array: In the recursive code, our base condition was when ind1 < 0 or ind2 < 0, but we can’t set the dp array’s index to -1. Therefore a hack for this issue is to shift every index by 1 towards the right.

Therefore, now the base case will be if(ind1==0 || ind2==0), return 0. So we will set dp array with 0 for ind1 = 0 and ind2 = 0.
- Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations. Keeping in mind the shifting of indexes, as for example S1[ind1] will be converted to S1[ind1-1].
- Returning the answer: At last dp[n][m] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.
Dry Run:
Define a DP table dp of size (m+1)*(n+1), where m and n are the lengths of str1 and str2:
Initialize the first row and first column with 0, because it is the base case, or we can initialize entire matrix as 0.
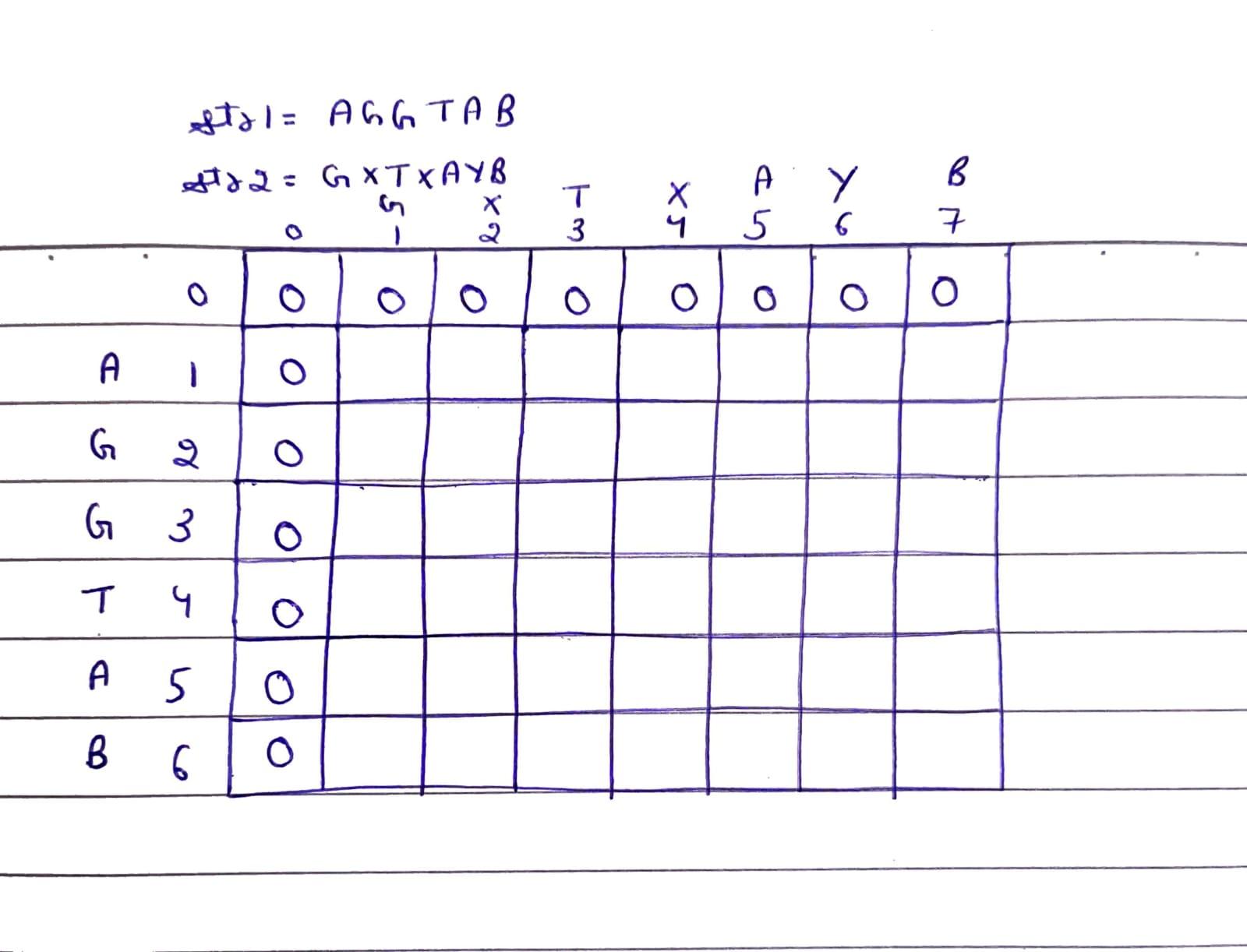
Fill the table from the cell (1, 1):
// Fill the table
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (X[i - 1] == Y[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1; // Match case
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); // Mismatch case
}
}
}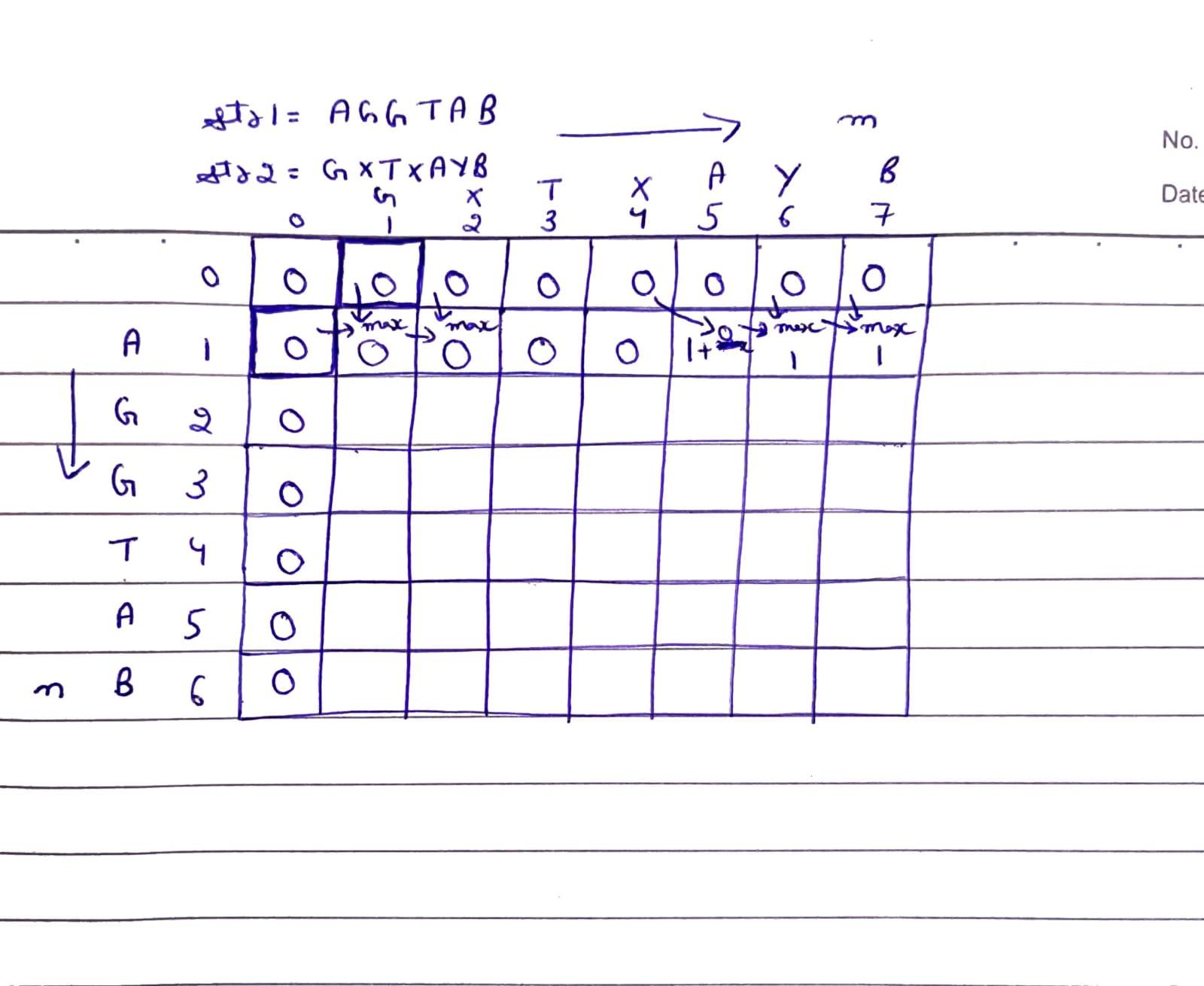
Final Table:
For X = "AGGTAB" and Y = "GXTXAYB", the DP table will look like this:
| G | X | T | X | A | Y | B | ||
|---|---|---|---|---|---|---|---|---|
| ** | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| G | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| G | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| T | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
| A | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 3 |
| B | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 |
Final answer is dp[m][n] = dp[6][7] = 4.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
/* Function to calculate the length
of the Longest Common Subsequence*/
int lcs(string str1, string str2) {
int n = str1.size();
int m = str2.size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1, -1));
// Initialize the base cases
for (int i = 0; i <= n; i++) {
dp[i][0] = 0;
}
for (int i = 0; i <= m; i++) {
dp[0][i] = 0;
}
// Fill in the DP table to calculate the length of LCS
for (int ind1 = 1; ind1 <= n; ind1++) {
for (int ind2 = 1; ind2 <= m; ind2++) {
// Characters match, increment LCS length
if (str1[ind1 - 1] == str2[ind2 - 1])
dp[ind1][ind2] = 1 + dp[ind1 - 1][ind2 - 1];
/* Characters don't match, consider
the maximum from left or above*/
else
dp[ind1][ind2] = max(dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]);
}
}
// Return the length of Longest Common Subsequence
return dp[n][m];
}
};
int main() {
string s1 = "acd";
string s2 = "ced";
//Create an instance of Solution class
Solution sol;
// Call the function to find and output
cout << "The Length of Longest Common Subsequence is " << sol.lcs(s1, s2) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(N*M),Nis the length of string S1 and M is the length of string S2. There are two nested loops which are running for N*M. - Space Complexity:
O(N*M), As a 2D array of size N*M is used.
4️⃣ Space Optimization
If we observe the relation obtained in tabulation approach, dp[ind1 - 1][ind2], dp[ind1][ind2 - 1]. We are using just two rows: dp[ind1-1][ ], dp[ind][ ] in order to calculate any row.
So we are not required to contain an entire array, we can simply have two rows 'prev' and 'cur' where prev corresponds to dp[ind-1] and cur to dp[ind].
After declaring 'prev' and 'cur', replace dp[ind-1] to prev and dp[ind] with cur in the tabulation code. Following the same logic of tabulation, we will calculate cur[ind] in each iteration and after the inner loop executes, we will set prev = cur, so that the cur row can serve as prev for the next index.
After end of the execution, return prev[m] as our answer, as it will hold the cumulative result of the overall calculation.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution{
public:
/* Function to calculate the length
of the Longest Common Subsequence*/
int lcs(string str1, string str2) {
int n = str1.size();
int m = str2.size();
/* Initialize two vectors to store the
current and previous rows of the DP table*/
vector<int> prev(m + 1, 0), cur(m + 1, 0);
/* Base case is covered as we have initialized
the prev and cur vectors to 0.*/
for (int ind1 = 1; ind1 <= n; ind1++) {
for (int ind2 = 1; ind2 <= m; ind2++) {
// Characters match, increment LCS length
if (str1[ind1 - 1] == str2[ind2 - 1])
cur[ind2] = 1 + prev[ind2 - 1];
else
cur[ind2] = max(prev[ind2], cur[ind2 - 1]);
}
// Update the previous row with current row
prev = cur;
}
// Return the length of Longest Common Subsequence
return prev[m];
}
};
int main() {
string s1 = "acd";
string s2 = "ced";
//Create an instance of Solution class
Solution sol;
// Call the function to find and output
cout << "The Length of Longest Common Subsequence is " << sol.lcs(s1, s2) << endl;
return 0;
}Complexity Analysis:
- Time Complexity:
O(N*M), N is the length of string S1 and M is the length of string S2. There are two nested loops which are running for N*M. - Space Complexity:
O(M), We are using an external array of size ‘M+1’ to store only two rows.
