Problem Statement

Given two binary trees, we need to determine whether they are identical or not. Two trees are considered identical if they have the same structure and the same node values in a one-to-one correspondence.

Concept

Identical binary trees have the same structure and values at corresponding nodes. To check for identically, we need to traverse both trees simultaneously and compare the nodes at each step.

Different Approaches

1️⃣ Recursive Approach:

Intuition:

To determine whether two binary trees are identical, one effective method is to traverse both trees simultaneously, comparing the values and structure of corresponding nodes at each step. The key idea is that two trees are identical if and only if every corresponding pair of nodes in the two trees have the same value and the same left and right subtrees. This requires ensuring that not only the values match, but that the structure of the trees (i.e., the presence or absence of left and right children) is also identical. Essentially, for the trees to be considered identical, the entire hierarchy from the root to the leaves must be the same.

We will start from the root of both trees and compare the current nodes. If they are equal, we move on to compare their left and right subtrees recursively. If any pair of corresponding nodes are not equal, the trees are not identical.

Approach:

1. Start at the root node of both trees (p and q). First, check if both nodes are null. If both are null, the current branches are identical up to this point, so return true. If only one of them is null or if their values differ, return false, as this means the trees are not identical.
2. Recursively compare the left subtree of p with the left subtree of q and the right subtree of p with the right subtree of q. At each step, ensure that both the structure (presence of children) and the node values match.
3. If all recursive checks for the left and right subtrees return true, then the trees are identical; otherwise, if any check fails, the trees are not identical. The final result will depend on the outcome of these recursive checks.

Dry Run:

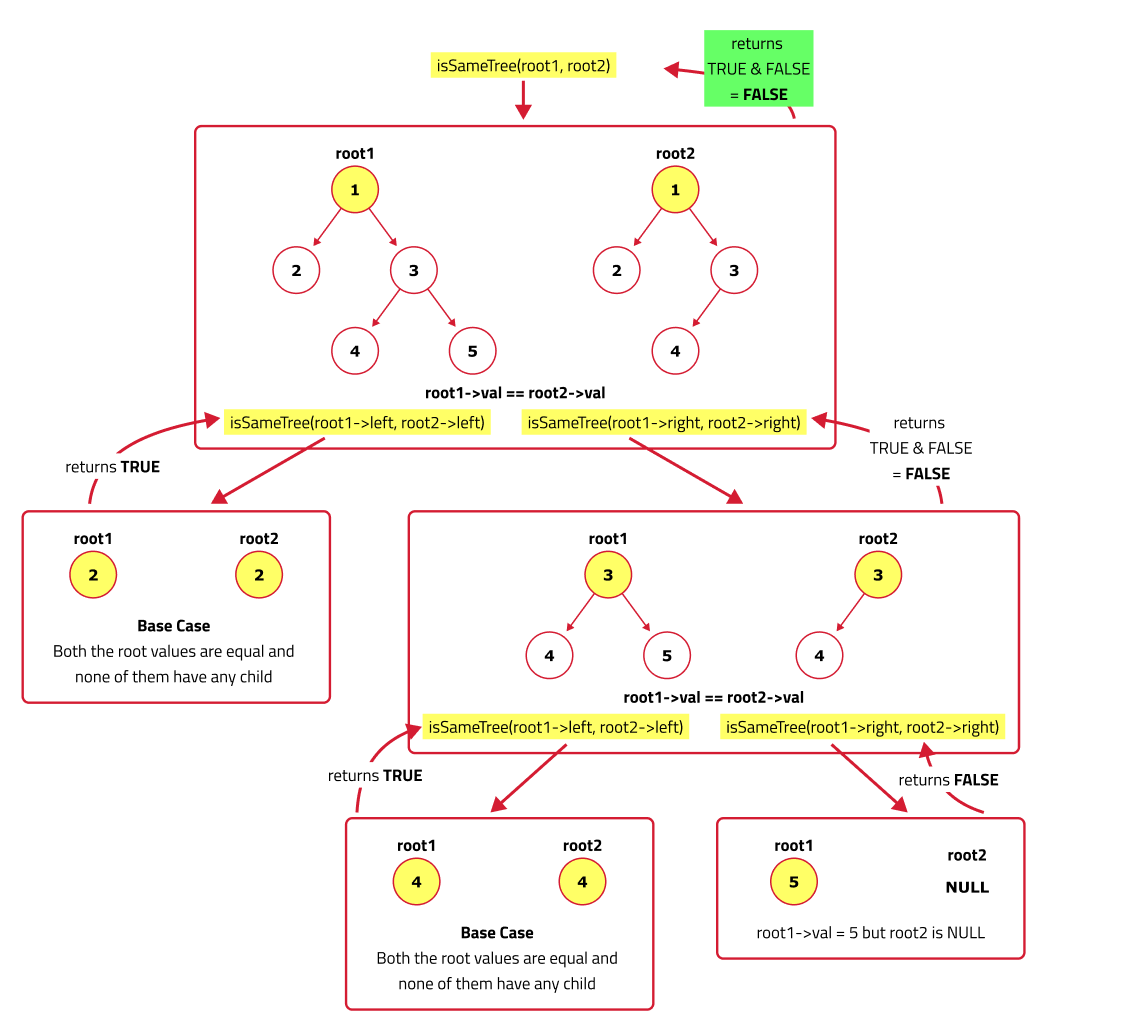
Code Implementation:

#include <bits/stdc++.h>
using namespace std;
// Definition of a binary tree node
struct TreeNode {
    int data;
    TreeNode *left, *right;
    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        // If both nodes are null, the trees are the same
        if (p == nullptr && q == nullptr) {
            return true;
        }

        // If one of the nodes is null, the trees are not the same
        if (p == nullptr || q == nullptr) {
            return false;
        }

        // If the values of the nodes are different, the trees are not the same
        if (p->data != q->data) {
            return false;
        }

        // Recursively check the left and right subtrees
        return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

int main() {
    // Example usage
    Solution solution;

    // Creating two sample trees
    TreeNode* tree1 = new TreeNode(1);
    tree1->left = new TreeNode(2);
    tree1->right = new TreeNode(3);

    TreeNode* tree2 = new TreeNode(1);
    tree2->left = new TreeNode(2);
    tree2->right = new TreeNode(3);

    // Checking if the trees are identical
    bool result = solution.isSameTree(tree1, tree2);
    cout << "Are the trees identical? " << result << endl;  // Output: 1 (true)

    // Clean up
    delete tree1->left;
    delete tree1->right;
    delete tree1;
    delete tree2->left;
    delete tree2->right;
    delete tree2;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N) 
  • Visit each node exactly once during the traversal, where N is the number of nodes in the tree.
• Space Complexity: O(h)
  • The space complexity is determined by the recursion stack, which can go as deep as the height of the tree h.