Problem Statement

Given two sorted arrays arr1 and arr2 of size m and n respectively, return the median of the two sorted arrays.

The median is defined as the middle value of a sorted list of numbers. In case the length of the list is even, the median is the average of the two middle elements.

Examples

Example 1:

Input: arr1 = [2, 4, 6], arr2 = [1, 3, 5]
Output: 3.5

Explanation: The array after merging arr1 and arr2 will be [ 1, 2, 3, 4, 5, 6 ]. As the length of the merged list is even, the median is the average of the two middle elements. Here two medians are 3 and 4. So the median will be the average of 3 and 4, which is 3.5.

Example 2:

Input: arr1 = [2, 4, 6], arr2 = [1, 3]
Output: 3

Explanation: The array after merging arr1 and arr2 will be [ 1, 2, 3, 4, 6 ]. The median is simply 3.

Different Approaches

1️⃣ Brute Force Approach

Intuition:

The extremely naive approach is to merge the two sorted arrays and then find the median of the final merged array. Given that the arrays are already sorted, the merge approach of the merge sort algorithm can be used. This approach iterates through both arrays, picking the smallest elements first and then the larger ones, resulting in a final sorted array.

Approach:

1. If the length of the merged array is even: The median is the average of the two middle elements. The index = (sizeOfMergedArray) / 2, median will be the sum of element at 'index' and the element at 'index-1' divided by 2.
2. If the length of the merged array is odd: index = (sizeOfMergedArray) / 2, median will be the element at ‘index’
3. Initialize an array of size equal to sum of size of 1st array and size of 2nd array to store the elements of the merged array.
4. Now, take two pointers i and j, where i points to the first element of arr1 and j points to the first element of arr2.
5. Next, initialize a while loop, which will run till any one of the pointers crosses the size of their respective array. If the element at pointer i is less than or equal to element at pointer j, then insert the element at pointer i in the merged array and increase i by 1. Otherwise, insert the element at j into the merged array and increase j by 1.
6. After that, the left-out elements from both arrays will be copied as it is into the merged array. Now, the merged array will be sorted, find the mediun based on the size of the array if it is even or odd. Finally, return the value of the median.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to find the median of two sorted arrays.
    double median(vector<int>& arr1, vector<int>& arr2) {
        // Size of two given arrays
        int n1 = arr1.size(), n2 = arr2.size();

        vector<int> merged;
        // Apply the merge step
        int i = 0, j = 0;
        while (i < n1 && j < n2) {
            if (arr1[i] < arr2[j]) merged.push_back(arr1[i++]);
            else merged.push_back(arr2[j++]);
        }

        // Copy the remaining elements
        while (i < n1) merged.push_back(arr1[i++]);
        while (j < n2) merged.push_back(arr2[j++]);

        // Find the median
        int n = n1 + n2;
        if (n % 2 == 1) {
            return (double)merged[n / 2];
        }

        double median = ((double)merged[n / 2] + (double)merged[(n / 2) - 1]) / 2.0;
        return median;
    }
};

int main() {
    vector<int> a = {1, 4, 7, 10, 12};
    vector<int> b = {2, 3, 6, 15};

    // Create an instance of the Solution class
    Solution sol;

    // Print the median of the two sorted arrays
    cout << "The median of two sorted arrays is " << fixed << setprecision(1)
         << sol.median(a, b) << '\n';

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N1+N2), where N1 and N2 are the sizes of the given arrays. As, both are arrays are being traversed linearly.
• Space Complexity: O(N1+N2), As, an extra array of size (N1+N2) is being used to solve this problem.

2️⃣ Better Approach

Intuition:

The idea is to optimize the extra space used in the brute-force approach by eliminating the array used to store the final merged result. Upon closer observation, it can be noticed that only the two middle elements at indices [(sum of the sizes of both array) / 2] and [((sum of the sizes of both arrays) / 2 - 1] are needed, rather than the entire merged array, to effectively solve the problem. Stick to the same basic approach,  but instead of storing elements in a separate array, use a counter called count to represent the imaginary third array's index. While traversing through the arrays, when count reaches either index (sum of size of both the arrays) / 2 or ((sum of both the arrays)/2 - 1, store that particular element. This way, the same goal can be achieved without using any extra space.

Dry Run:

       +-----+-----+-----+
arr1 = |  2  |  4  |  6  |
       +-----+-----+-----+
arr2 = |  1  |  3  |  5  |
       +-----+-----+-----+
          0     1     2

       +-----+-----+-----+
arr1 = |  2  |  4  |  6  |
       +-----+-----+-----+
arr2 = |  1  |  3  |  5  |
       +-----+-----+-----+
          0     1     2

n1 = arr1.size = 3
n2 = arr2.size = 3
n = n1 + n2 = 6

// Required indices for median calculation
index2 = n / 2
       = 6 / 2 = 3
index1 = index2 - 1
       = 3 - 1
       = 2

count = 0
index1Element = -1
index2Element = -1

Merge Step:

i = 0, j = 0
count = 0
index2 = 3
index1 = 2
index1Element = -1
index2Element = -1
i < n1 && j < n2
0 < 3 && 0 < 3
True
     Check if arr1[i] < arr[j]
              2 < 1
              False
         if()

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to find the median of two sorted arrays.
    double median(vector<int>& arr1, vector<int>& arr2) {
        // Size of two given arrays
        int n1 = arr1.size(), n2 = arr2.size();
        int n = n1 + n2; // Total size

        // Required indices for median calculation
        int ind2 = n / 2;
        int ind1 = ind2 - 1;
        int cnt = 0;
        int ind1el = -1, ind2el = -1;

        // Apply the merge step
        int i = 0, j = 0;
        while (i < n1 && j < n2) {
            if (arr1[i] < arr2[j]) {
                if (cnt == ind1) ind1el = arr1[i];
                if (cnt == ind2) ind2el = arr1[i];
                cnt++;
                i++;
            } else {
                if (cnt == ind1) ind1el = arr2[j];
                if (cnt == ind2) ind2el = arr2[j];
                cnt++;
                j++;
            }
        }

        // Copy the remaining elements
        while (i < n1) {
            if (cnt == ind1) ind1el = arr1[i];
            if (cnt == ind2) ind2el = arr1[i];
            cnt++;
            i++;
        }
        while (j < n2) {
            if (cnt == ind1) ind1el = arr2[j];
            if (cnt == ind2) ind2el = arr2[j];
            cnt++;
            j++;
        }

        // Find the median
        if (n % 2 == 1) {
            return (double) ind2el;
        }

        return (double) ((double) (ind1el + ind2el)) / 2.0;
    }
};

int main() {
    vector<int> a = {1, 4, 7, 10, 12};
    vector<int> b = {2, 3, 6, 15};

    // Create an instance of the Solution class
    Solution sol;

    // Print the median of the two sorted arrays
    cout << "The median of two sorted arrays is " << fixed << setprecision(1)
         << sol.median(a, b) << '\n';

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N1 + N2), where N1 and N2 are the sizes of the given arrays, As both arrays are being traversed linearly.
• Space Complexity: O(1)

3️⃣ Optimal Approach (Binary Search)

Intuition:

The key idea is to use the Binary Search algorithm to optimize our approach. Binary Search works by efficiently determining which half of the search space can be eliminated based on a specific condition, reducing the search space by half at each step.

In this problem, we'll start by addressing the case where the combined size of both arrays is even. Once that is solved, we’ll extend the approach to handle the odd case. Let’s explore how to apply Binary Search systematically to this scenario.

For even:

Observation: Let n represent the total size of both arrays comnined. The two halves of the merged array will each contain n/2 elements.

• Each half consists of x elements from the first array.
• While (n/2) - x elements from the second array.

Unique Configurations of Halves: By selecting different values for x, we can generate different combinations of left and right halves. Here, x represents the number of elements chosen from the first array for a specific partition.

Median as a Partition Point: On closer examination, we observe that the median naturally divides the final merged array into two.

In a valid merged array, the configuration of the two halves are unique. To achieve this, we can explore different values of x, where x is the number of elements taken from arr1[] for particular left half.

Key Insight: There’s no need to construct both halves explicitly. Once the left half is correctly formed, the right half is automatically determined by the remaining elements. Thus, our focus will solely be on constructing a valid configuration for the left half.

How to Form All Configurations of the Left Half:

• The left half will consist of x elements from arr1[] and (n/2) - x elements from arr2[].
• The variable x determines how many elements are taken from arr1[].
• The minimum value of x is 0, and the maximum value is n1 (the length of arr1[]).

For all possible values of x in the range [0, n1], we will attempt to construct the left half. After forming each configuration, we will verify whether it satisfies the condition of a valid partition.

Check if the formed left half is valid:

For a valid left half, the merged array will always be sorted. So, if the merged array containing the formed left half is sorted, the formation is valid. How to check if the merged array is sorted without forming the array: In order to check we will consider 4 elements, i.e. l1, l2, r1, r2.

• l1 = the maximum element belonging to arr1[] of the left half.
• l2 = the maximum element belonging to arr2[] of the left half.
• r1 = the minimum element belonging to arr1[] of the right half.
• r2 = the minimum element belonging to arr2[] of the right half.

How to apply binary search to form the left half:

We will check the formation of the left half for all possible values of x. Now, we know that the minimum possible value of x is 0 and the maximum is n1(i.e. The length of the considered array). Now the range is sorted. So, we will apply the binary search on the possible values of x i.e. [0, n1].

How to eliminate halves based on the values of x:

Binary search works by eliminating the halves in each step. Upon closer observation, we can eliminate the halves based on the following conditions:

• If l1 > r2: This implies that we have considered more elements from arr1[] than necessary. So, we have to take less elements from arr1[] and more from arr2[]. In such cases we should try smaller values of x. To achieve this, we will eliminate the right half (high = mid - 1).
• If l2 > r1: This implies that we have considered more elements from arr2[] than necessary. So, we have to take less elements from arr2[] and more from arr1[]. In such a scenario, we should try bigger values of x. To achieve this, we will eliminate the left half (low = mid + 1).

We have learned how to use binary search for that (n1 + n2) is even:

Now for Odd:

If (n1 + n2) is odd: In the case of even, we have considered the length of the left half as (n1 + n2) / 2. In this case, the length will be (n1 + n2 + 1) / 2. This much change is enough to handle the case of odd. The rest of the things will be completely the same. As in the code, division refers to integer division, this modified formula (n1+n2+1) / 2 will be valid for both cases of odd and even.

What will be the median:

• If l1 <= r2 && l2 <= r1: This condition assures that we have found the correct elements.
• If (n1+n2) is odd: The median will be max(l1, l2). Otherwise, median = (max(l1, l2) + min(r1, r2)) / 2.0

Note: We are applying binary search on the possible values of x i.e. [0, n1]. Here n1 is the length of arr1[]. Now, to further optimize it, we will consider the smaller array as arr1[]. So, the actual range will be [0, min(n1, n2)].

Approach:

1. First, make sure that the arr1 is the smaller array. If not by default, just swap the arrays. Our main goal is to consider the smaller array as arr1[]. Calculate the length of the left half as (n1+n2+1) / 2.
2. Initialize two pointers: low and high, low will point to 0 and the high will point to n1(i.e. The size of arr1). Calculate the ‘mid1’ i.e. x and ‘mid2’ i.e. [left-x]. Now, inside the loop, calculate the value of ‘mid1’ using the following formula, mid1 = (low+high) // 2 ( ‘//’ refers to integer division) and mid2 = left-mid1.
3. Calculate l1, l2, r1, and r2: Generally,
   1. l1 = arr1[mid1-1]
   2. l2 = arr2[mid2-1]
   3. r1 = arr1[mid1]
   4. r2 = arr2[mid2]
4. The possible values of ‘mid1’ and ‘mid2’ might be 0 and n1 and n2 respectively. So, to handle these cases, store some default values for these four variables. The default value for l1 and l2 will be INT_MIN and for r1 and r2, it will be INT_MAX.
5. Eliminate the halves based on the following conditions:
   1. If l1 is less than or equal to r2 and l2 less than or equal to r1, the answer has been found.
      1. If sum of size of the arrays is odd, return the median as maximum of (l1, l2). Otherwise, return median as the average of max(l1, l2) + min(r1, r2).
   2. If l1 is greater than r2. This implies that more elements from arr1 have been considered than needed. So, try to take less elements from arr1 and more from arr2. In such a scenario, take smaller values of x. To achieve this, eliminate the right half (high = mid1-1).
   3. If l2 greater than r1. This implies that we have considered more elements from arr2 than needed. So, try to take less elements from arr2 and more from arr1. In such a scenario, take bigger values of x. To achieve this, eliminate the left half (low = mid1+1).
6. Finally, outside the loop, include a dummy return statement just to avoid warnings or errors.

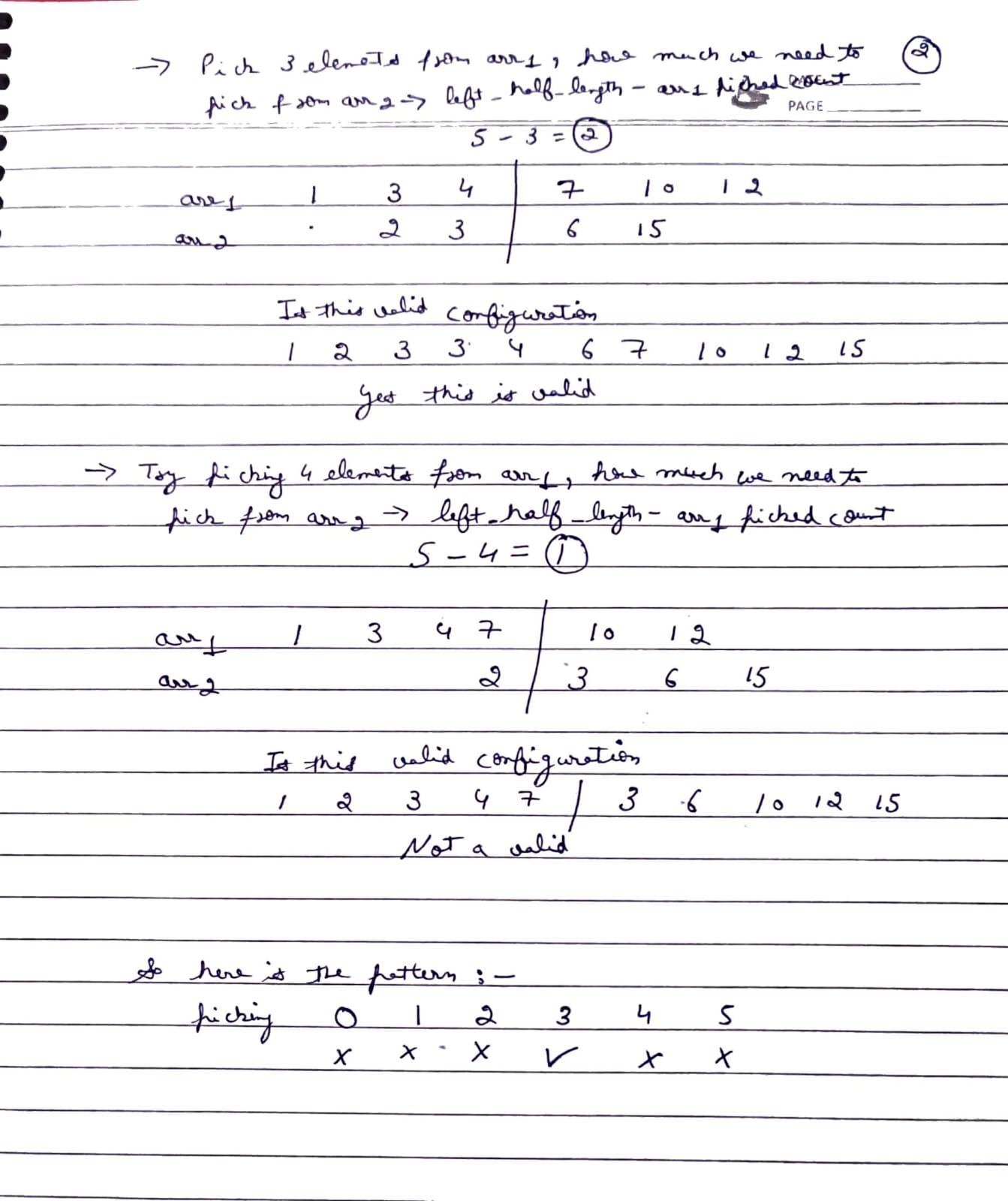
Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    //Function to find the median of two sorted arrays.
    double median(vector<int>& arr1, vector<int>& arr2) {
        // Size of two given arrays
        int n1 = arr1.size(), n2 = arr2.size();

        /* Ensure arr1 is not larger than 
        arr2 to simplify implementation*/
        if (n1 > n2) return median(arr2, arr1);

        int n = n1 + n2;
        
        // Length of left half
        int left = (n1 + n2 + 1) / 2; 

        // Apply binary search
        int low = 0, high = n1;
        while (low <= high) {
            
            // Calculate mid index for arr1
            int mid1 = (low + high) >> 1; 
            
            // Calculate mid index for arr2
            int mid2 = left - mid1; 

            // Calculate l1, l2, r1, and r2
            int l1 = (mid1 > 0) ? arr1[mid1 - 1] : INT_MIN;
            int r1 = (mid1 < n1) ? arr1[mid1] : INT_MAX;
            int l2 = (mid2 > 0) ? arr2[mid2 - 1] : INT_MIN;
            int r2 = (mid2 < n2) ? arr2[mid2] : INT_MAX;

            if (l1 <= r2 && l2 <= r1) {
                // If condition for finding median
                if (n % 2 == 1) return max(l1, l2);
                else return (max(l1, l2) + min(r1, r2)) / 2.0;
            } 
            else if (l1 > r2) {
                // Eliminate the right half of arr1
                high = mid1 - 1;
            } else {
                // Eliminate the left half of arr1
                low = mid1 + 1;
            }
        }
        // Dummy statement
        return 0; 
    }
};

int main() {
    vector<int> arr1 = {1, 4, 7, 10, 12};
    vector<int> arr2 = {2, 3, 6, 15};

    // Create an instance of the Solution class
    Solution sol;

    // Print the median of the two sorted arrays
    cout << "The median of two sorted arrays is " << fixed << setprecision(1)
         << sol.median(arr1, arr2) << '\n';

    return 0;
}

Complexity Analysis:

• Time Complexity: O(log(min(N1, N2))), where N1 and N2 are the sizes of two given arrays. As, binary search is being applied on the range [0, min(N1, N2)].
• Space Complexity: O(1)