Problem Statement

Design a data structure that follows the constraints of Least Recently Used (LRU) cache.

• Implement the LRUCache class:
  • LRUCache(int capacity): We need to initialize the LRU cache with positive size capacity.
  • int get(int key): Returns the value of the key if the key exists, otherwise return -1.
  • void put(int key,int value): Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.
  • The functions get and put must each run in O(1) average time complexity.

Examples

Example 1:

Input:
 ["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
 [ [2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4] ]
Output:
 [null, null, null, 1, null, -1, null, -1, 3, 4]

Explanation:
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1);  // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2);  // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1);  // return -1 (not found)
lRUCache.get(3);  // return 3
lRUCache.get(4);  // return 4

Input:
["LRUCache", "put", "put", "get", "put", "get", "put", "get"]
[[1], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [3]]
Output:
[null, null, null, -1, null, -1, null, -1]

Explanation:
LRUCache lRUCache = new LRUCache(1);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // evicts key 1, cache is {2=2}
lRUCache.get(1);  // returns -1 (not found)
lRUCache.put(3, 3); // evicts key 2, cache is {3=3}
lRUCache.get(2);  // returns -1 (not found)
lRUCache.put(4, 4); // evicts key 3, cache is {4=4}
lRUCache.get(3);  // returns -1 (not found)

Different Approaches

1️⃣ Hashmaps and Doubly Linked List

Intuition:

As the name suggests, the data items (key-value pairs) that are least recently used will be staying in the cache memory. To mark the data items as recently used, a doubly linked list can be used. The most recently used data item will be placed in the front and the least recently used data item will be placed at the end of the doubly linked list.

Why using a Doubly Linked List?

Because doubly linked list data structure makes the insertion and deletion operation on data items in constant time while making sure the order of data items remains.

But in order to implement the get method for LRU cache, the searching operation will take linear time where each data-item needs to be checked. To improve the complexity of get method, a hashmap can be used to store the key and the address of node containing the key (if it exists).

This way, the two methods can be implemented in constant time:

• Get method: Using hashmap, it can be found whether a key exists in the doubly linked list. If it exists, the corresponding value can be returned using the address of node, otherwise, -1 can be returned.
• Put method: If the key exists in the doubly linked list, its value can be updated. Otherwise, the least recently used data-item can be removed and the current key-value pair can be inserted.

Approach:

1. The cache is initialized with a given capacity. Two dummy nodes, head and tail, are created to mark the start and end of cache. The head's next points to the tail, and the tail's previous points to the head.
2. Get operation:
   1. Check if the key exists in the hash map.
   2. If the key is present, retrieve the corresponding node, move it to the front (mark it as recently used), and return its value.
   3. If the key is not present, return -1.
3. Put operation:
   1. Check if the key already exists in the hash map.
   2. If the key is present, update the node's value, move it to the front (mark it as recently used). If the key is not present, check if the cache has reached its capacity.
   3. If at capacity, remove the least recently used node (node right before the tail) from both the hash map and the doubly linked list.
   4. Insert the new key-value pair as a new node at the front (mark it as recently used) and add it to the hash map.
4. There are two helper functions:
   1. DeleteNode: This function removes a given node from the doubly linked list by adjusting the pointers of its previous and next nodes.
   2. InsertAfterHead: This function inserts a given node right after the head, marking it as the most recently used.

Dry Run:

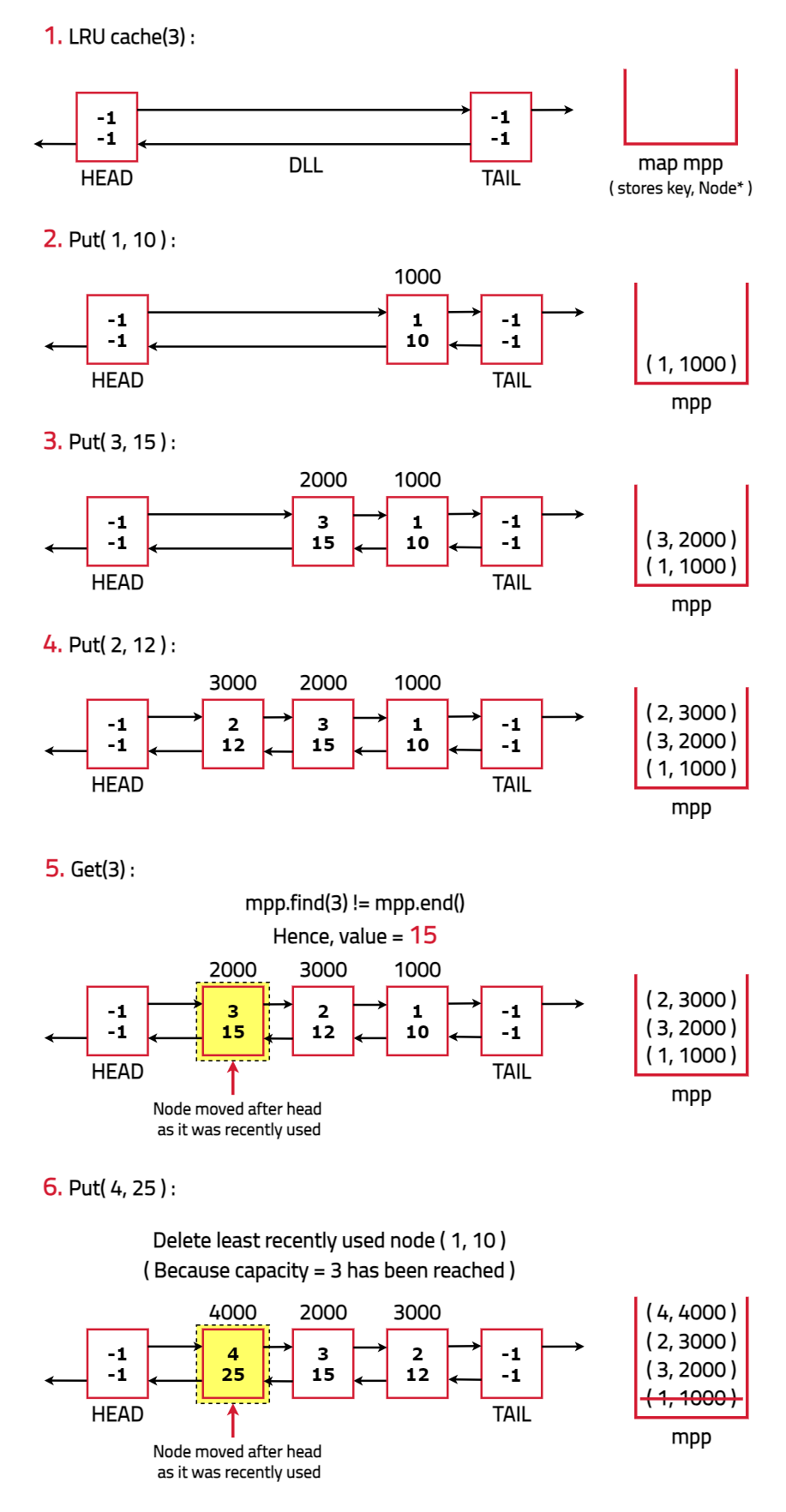
Code:

#include <bits/stdc++.h>
using namespace std;

/* Class to implement Nodes
of a doubly linked list */
class Node {
public:
	int key, val;
	Node* next;
	Node* prev;
    
    // Constructors
	Node() {
		key = val = -1;
		next = prev = NULL;
	}

	Node(int k, int value) {
		key = k;
		val = value;
		next = prev = NULL;
	}
};

// Class implementing LRU cache
class LRUCache {
private:

	map <int, Node*> mpp; // Map data structure
	int cap; // Capacity
	Node* head; // Dummy head pointer
	Node* tail; // Dummy tail pointer

	/* Private method to delete node
	from doubly linked list */
	void deleteNode(Node* node) {

		// Get the previous and next pointers
		Node* prevNode = node-> prev;
		Node* nextNode = node-> next;

		// Remove pointers to node
		prevNode-> next = nextNode;
		nextNode-> prev = prevNode;
	}

	// Private method to insert node after head
	void insertAfterHead(Node* node) {

		Node* nextNode = head-> next;
		head-> next = node;
		nextNode-> prev = node;
		node-> prev = head;
		node-> next = nextNode;
	}

public:
	// Method to initialise cache with given capacity
	LRUCache(int capacity) {
		cap = capacity; // Set the capacity
		mpp.clear(); // Clear the cache

		head = new Node();
		tail = new Node();

		// Make the connections
		head-> next = tail;
		tail-> prev = head;
	}

	// Method to get the key from cache
	int get(int key_) {
		// Return -1 if it is not present in cache
		if(mpp.find(key_) == mpp.end())
			return -1;

		Node* node = mpp[key_]; // Get the node
		int val = node->val; // Get the value

		// Delete the node
		deleteNode(node);
		/* Insert this node to front
		as it was recently used */
		insertAfterHead(node);

		// Return the stored value
		return val;
	}

	/* Method to update value is key exists,
	otherwise insert the key-value pair */
	void put(int key_, int value) {

		// Update the value if key is already present
		if(mpp.find(key_) != mpp.end()) {
		    
			Node* node = mpp[key_]; // Get the node
			node->val = value; // Update the value
            
			// Delete the node
			deleteNode(node);
			
			/* Insert this node to front
			as it was recently used */
			insertAfterHead(node);
			
			return;
		}

		// Check if the capacity limit has reached
		if(mpp.size() == cap) {

			// Get the least recently used node
			Node* node = tail->prev;

			// Delete node from map
			mpp.erase(node-> key);

			// Delete node from doubly linked list
			deleteNode(node);
		}

		// Create a new node
		Node* newNode = new Node(key_, value);
		
		// Insert it in map
		mpp[key_] = newNode;

		// Insert in doubly linked list
		insertAfterHead(newNode);
	}
};


int main() {
	// LRU Cache
	LRUCache cache(2);

	// Queries
	cache.put(1, 1);
	cache.put(2, 2);
	cout << cache.get(1) << " ";
	cache.put(3, 3);
	cout << cache.get(2) << " ";
	cache.put(4, 4);
	cout << cache.get(1) << " ";
	cout << cache.get(3) << " ";
	cout << cache.get(4) << " ";

	return 0;
}

Complexity Analysis:

• Time Complexity:O(N) (where N is the number of queries)
  • Since the Put and Get method takes an average of constant time, the overall complexity to process all the queries is O(N) time.
• Space Complexity:O(cap) (where cap is the capacity of the LRU cache)
  • Since the doubly linked list can store at most of the capacity number of key-value pairs, this takes O(cap) space.