Understanding Tree Data Structure
A tree is a non-linear, hierarchical data structure in computer science that consists of nodes connected by edges. Each node stores data and may point to other nodes. A tree starts from a root node and expands to child nodes, where each child may have its own children, forming a parent-child relationship.
A tree is called a non-linear data structure because the elements (nodes) cannot be accessed in a single continuous sequence as they can in linear data structures like arrays or linked lists.
In a tree, data is organized in a hierarchical and branching manner, which requires multiple paths or recursive traversal methods to access all elements.
Key Characteristics of a Tree:
A (Root)
/ \
B C
/ \ / \
D E F G
(Leaf) (Leaf)
Root: A
Nodes: A, B, C, D, E, F, G
Edges: A→B, A→C, B→D, B→E, C→F, C→G
Children: B and C are children of A; D and E are children of B; F and G are children of C
Parents: A is the parent of B and C; B is the parent of D and E; C is the parent of F and G
Siblings: B and C; D and E; F and G
Leaf Nodes: D, E, F, G (because they have no children)
Subtree rooted at B: B, D, E
Height of the tree: 2
Depth of node D: 2
1. Root
- The topmost node in the tree is called the root.
- It is the starting point of the tree and has no parent.
2. Node
- Each element in the tree is called a node.
- A node can store data and connect to other nodes via edges.
3. Edge
- An edge is a connection between two nodes.
- It shows the relationship between a parent and its children.
4. Child
- A child node is a node directly connected to another node (its parent) by an edge.
- In the tree example above, nodes B and C are children of A.
5. Parent
- A parent node is one that has at least one child.
- In the tree example above, A is the parent of B and C.
6. Ancestors
- Nodes that lie on the path from a particular node to the root node. They are the nodes encountered while moving upwards from a specific node through its parent nodes until reaching the root of the tree.
- Going up from a child or leaf.
- Example: B, A are ancestors of D. A, C are ancestors of G.
7. Descendants
- A descendant of a any node that lies in the subtree rooted at that node. This includes children, grandchildren, great-grandchildren, and so on.
- Going down from top root.
- Descendants of A (Root):
- All other nodes: B, C, D, E, F, G.
- Descendants of B:
- D and E.
- Descendants of C:
- F and G.
- Descendants of D, E, F, G (Leaves):
- Since these are leaf nodes, they have no descendants.
8. Sibling
- Siblings are nodes that share the same parent.
- In the tree, B and C are siblings.
9. Leaf Node
- A leaf node is a node that has no children.
- In the tree, D, E, F, and G are leaf nodes.
10. Subtree
- A subtree is any node in the tree along with its descendants.
- The subtree rooted at B includes nodes B, D, and E.
11. Height of Tree
- The height of a tree is the number of edges from the root to the farthest leaf.
- In the tree below, the height is 2 (the path from A to D or E).
12. Depth of Node
- The depth of a node is the number of edges from the root to that node.
- In the tree, the depth of node D is 2.
13. Degree of a Node
- The degree of a node is the number of children that a node has.
- A node with no children has a degree of 0 (this is typically a leaf node).
- A node with multiple children has a degree equal to the number of those children.
A
/ \
B C
/ \
D E
The degree of node A is 2 (since A has two children: B and C).
The degree of node B is 2 (since B has two children: D and E).
The degree of node C is 0 (since C has no children and is a leaf).
The degree of nodes D and E is 0 (since they are leaf nodes).14. Degree of a Tree
- The degree of a tree is the maximum degree of any node within the tree.
- In other words, it is the largest number of children that any single node in the tree has.
A
/ \
B C
/ \
D E
The degree of the tree is 2, since the maximum degree of any node in the tree is 2 (both A and B have two children).Binary Tree Representation in C/C++
1️⃣ Using Structure:
// Define a structure for the binary tree node
struct Node {
int data;
Node* left; // Pointer to the left child
Node* right; // Pointer to the right child
// Constructor to create a new node
Node(int value) {
data = value;
left = nullptr;
right = nullptr;
}
};
int main() {
// Creating a new node for the root of the
// binary tree using dynamic allocation
Node* root = new Node(1);
// Creating left and right child
// nodes for the root node
root->left = new Node(2);
root->right = new Node(3);
// Creating a right child node for
// the left child node of the root
root->left->right = new Node(5);
}2️⃣ Using Class:
class Node {
public:
int data;
Node* left;
Node* right;
// Constructor to create a new node
Node(int value) {
data = value;
left = nullptr;
right = nullptr;
}
};
int main() {
// Creating a new node for the root of the
// binary tree using dynamic allocation
Node* root = new Node(1);
// Creating left and right child
// nodes for the root node
root->left = new Node(2);
root->right = new Node(3);
// Creating a right child node for
// the left child node of the root
root->left->right = new Node(5);
}Types of Trees:
1 Binary Tree
Each node has at most two children, referred to as the left and right children.
2 Binary Search Tree (BST):
A binary tree where the left child contains values less than the parent, and the right child contains values greater than the parent.
- All nodes in the left subtree contain values less than the node.
- All nodes in the right subtree contain values greater than the node.
Example:
10
/ \
5 20
/ \
3 7
Types of Binary Trees
1 Strict Binary Tree:
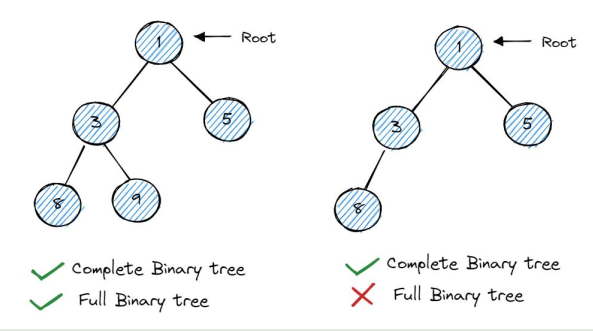
A binary tree is called strict binary tree if each node has exactly two children or no children.
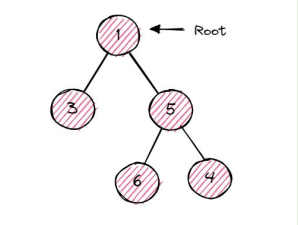
2 Full Binary Tree:
A binary tree in which each node have two children and all the leaf nodes are on the same level.
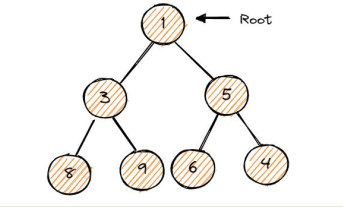
3 Complete Binary Tree:
A binary tree in which all the levels are completely filled except possibly the lowest one, which is filled from the left. The nodes in the last node are as far left as possible.
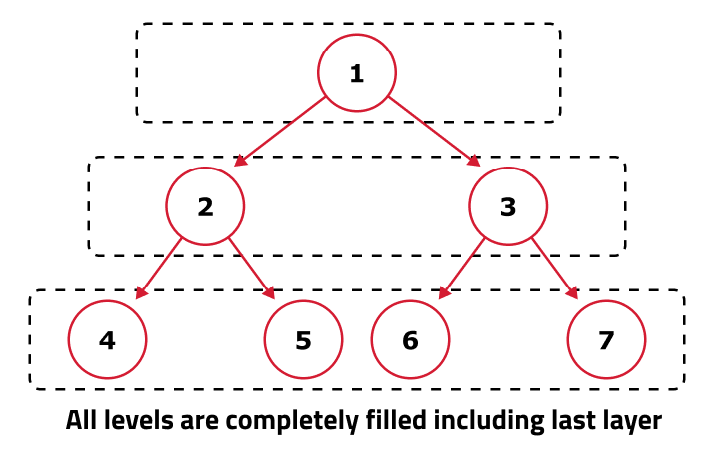
4 Perfect Binary Tree:
A binary tree in which all interior nodes have two children, and all leaf nodes are at the same level.
A type of binary tree where all leaf nodes are at the same level and the number of leaf nodes is maximized for that level. Every node in a perfect binary tree has either zero or two children. This means that every internal node (non-leaf node) has exactly two children and all leaf nodes are the same level.
5 Balanced Binary Tree:
A binary tree in which the height of the left and right subtrees of every node differ by at most 1.
Subtypes:
- AVL Tree:
- A self-balancing binary search tree where the height difference between the left and right subtrees of every node is at most 1.
- Red-Black Tree:
- A self-balancing binary search tree where nodes have an additional color property (red or black) that ensures balance.
5 Skew Binary Tree:
A binary tree in which every parent has exactly one child, making it effectively a linked list.
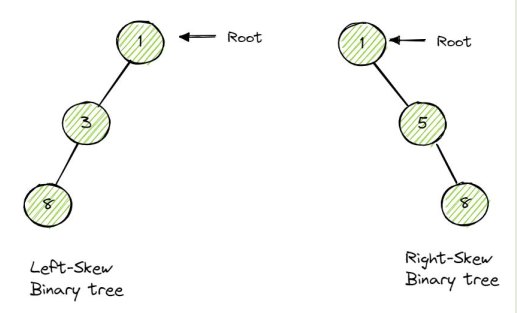
Real-World Use Cases
- File Systems (hierarchical directory structures)
- DOM Tree in HTML
- Trie for autocomplete and spell-check
- Parse trees in compilers
- Routing tables, decision trees, game trees

