Problem Statement
Given the root of a binary tree, return the inorder traversal of its nodes' values.
Inorder traversal follows the Left → Root → Right sequence.
In-order traversal follows the left-root-right sequence, meaning it starts from the left subtree, then moves to the root, and finally explores the right subtree. This traversal pattern is particularly useful for binary trees, where each node has at most two children. The in-order traversal helps retrieve the elements of a binary search tree in sorted order.
LeetCode:
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 ≤ Node.val ≤ 100
Examples
Example 1:
1
/ \
2 3
/ \
4 5
Output: 4 2 5 1 3Different Approach
1️⃣ Recursion Approach:
Intuition:
The in-order traversal is often implemented using recursion, taking advantage of the natural recursive structure of trees. The algorithm is as follows:
- Traverse the left subtree in-order.
- Visit the current node.
- Traverse the right subtree in-order.
This recursive process continues until all nodes are visited. The base case of the recursion is reaching a null (or empty) subtree, indicating the end of the traversal.
Approach:
To perform the in-order traversal, we follow these steps:
- First, we check if the current node is null. If it is, we return because there is nothing to process.
- If the current node is not null, we move to the left child of the current node and repeat the process.
- Once we reach a node with no left child, we process the current node.
- After processing the current node, we move to the right child and apply the same steps.
Dry Run:
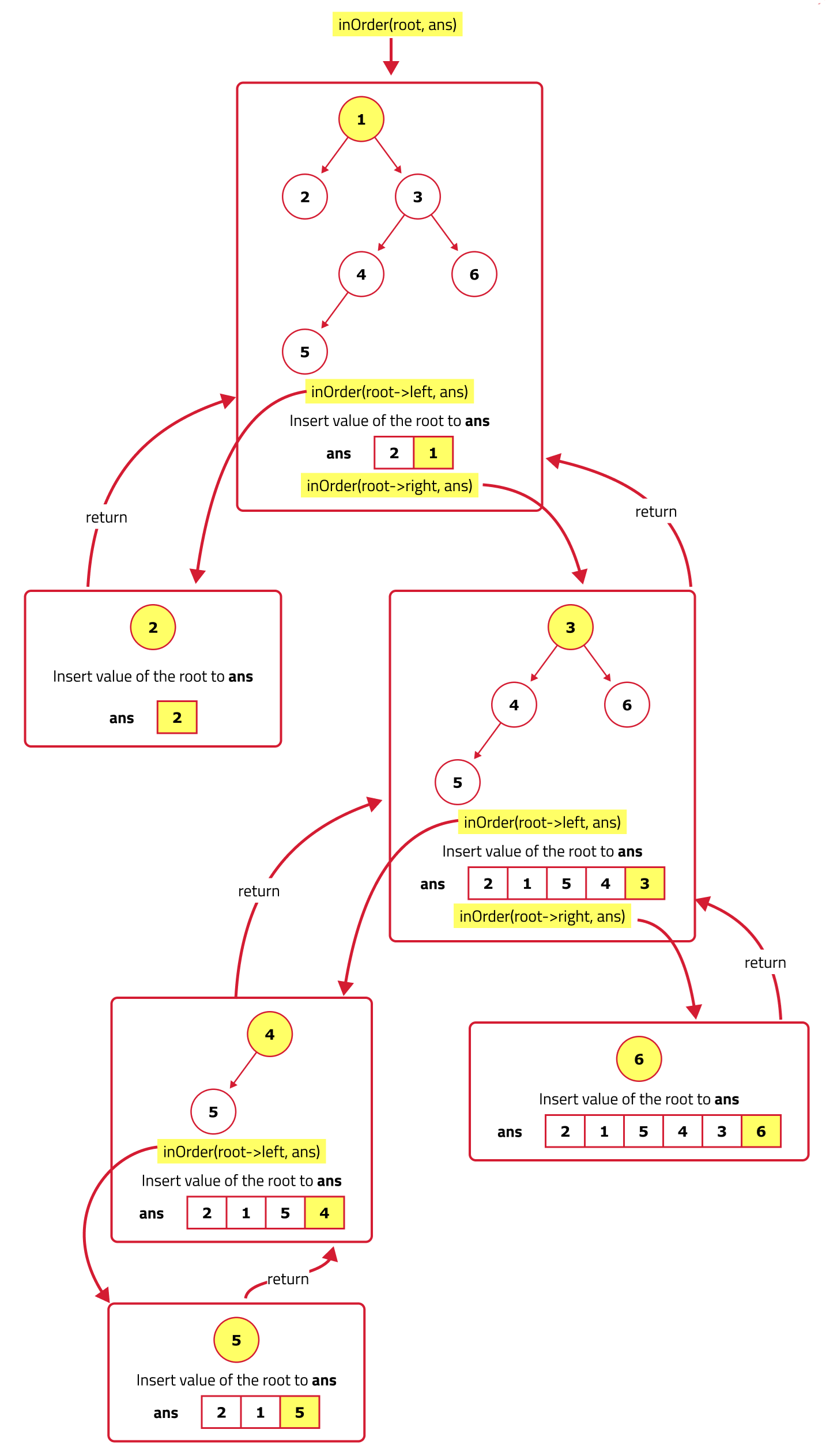
Code:
Let's implement the in-order traversal algorithm in C++:
#include <iostream>
#include <vector>
using namespace std;
// TreeNode structure for the binary tree
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
// Constructor to initialize
// the TreeNode with a value
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution{
private:
// Function to perform inorder traversal
// of the tree and store values in 'arr'
void recursiveInorder(TreeNode* root, vector<int> &arr){
// If the current Tree is NULL
// (base case for recursion), return
if(root == nullptr){
return;
}
// Recursively traverse the left subtree
recursiveInorder(root->left, arr);
// Push the current TreeNode's
// value into the vector
arr.push_back(root->data);
// Recursively traverse
// the right subtree
recursiveInorder(root->right, arr);
}
public:
// Function to initiate inorder traversal
// and return the resulting vector
vector<int> inorder(TreeNode* root){
// Create an empty vector to
// store inorder traversal values
vector<int> arr;
// Call the inorder traversal function
recursiveInorder(root, arr);
// Return the resulting vector
// containing inorder traversal values
return arr;
}
};
// Main function
int main()
{
// Creating a sample binary tree
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
Solution sol = Solution();
// Getting inorder traversal
vector<int> result = sol.inorder(root);
// Displaying the inorder traversal result
cout << "Inorder Traversal: ";
// Output each value in the
// inorder traversal result
for(int val : result) {
cout << val << " ";
}
cout << endl;
return 0;
}
Complexity Analysis:
- Time Complexity: The time complexity of the in-order traversal is
O(n), where n is the number of nodes in the tree. This is because each node is visited exactly once. - Space Complexity: The space complexity is
O(h), where h is the height of the tree. In the worst case, for a skewed tree, the height can be equal to the number of nodes, resulting inO(n)space complexity.
2️⃣ Iterative Approach:
Intuition:
The iterative approach to in-order traversal uses a stack to mimic the behavior of recursion. By using a stack, we can keep track of nodes we need to process, allowing us to traverse the tree without the need for recursive calls. This approach follows the in-order sequence: visit the left subtree, process the root, and then visit the right subtree. The stack helps manage this sequence effectively by storing nodes as we traverse down the left side of the tree and then processing them in the correct order.
Approach:
- Initialize a Stack:
- Create an empty stack to keep track of nodes.
- Traverse the Tree:
- Start with the root node.
- While the current node is not null or the stack is not empty:
- Traverse the left subtree:
- Push each node onto the stack until reaching the leftmost node.
- Visit the current node:
- Pop the top node from the stack.
- Process the node (e.g., prints its value).
- Move to the right subtree:
- Set the current node to its right child.
- Traverse the left subtree:
- Repeat Until Completion:
- Continue the process until the stack is empty and the current node is null.
Code:
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
// Define the TreeNode structure
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
// Function to perform inorder traversal
// of a binary tree iteratively
vector<int> inorder(TreeNode* root){
// Initialize a stack to track nodes
stack<TreeNode*> st;
// Start from the root node
TreeNode* node = root;
// Initialize a vector to store
// inorder traversal result
vector<int> inorder;
// Start an infinite
// loop for traversal
while(true){
// If the current node is not NULL
if(node != NULL){
// Push the current
// node to the stack
st.push(node);
// Move to the left child
// of the current node
node = node->left;
}
else{
// If the stack is empty,
// break the loop
if(st.empty()){
break;
}
// Retrieve a node from the stack
node = st.top();
// Remove the node from the stack
st.pop();
// Add the node's value to
// the inorder traversal list
inorder.push_back(node->val);
// Move to the right child
// of the current node
node = node->right;
}
}
// Return the inorder
// traversal result
return inorder;
}
};
int main() {
// Creating a binary tree
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
// Initializing the Solution class
Solution sol;
// Getting the inorder traversal
vector<int> result = sol.inorder(root);
// Displaying the inorder traversal result
cout << "Inorder Traversal: ";
for (int val : result) {
cout << val << " ";
}
cout << endl;
return 0;
}Complexity Analysis:
- Time Complexity:
O(n)where n is the number of nodes in the tree. As each node is visited exactly once. - Space Complexity: In the worst case (skewed tree), the height can be equal to the number of nodes, resulting in
O(n)space complexity.

