What is Pascal's Triangle?

Pascal's Triangle is a triangular array of numbers where each number is the sum of the two numbers directly above it. The triangle starts with a single 1 at the top, and the edges of the triangle are always 1. Every number inside the triangle is the sum of the two numbers directly above it.

Structure of Pascal’s Triangle

1. The first row of Pascal’s Triangle is always 1.
2. The second row is 1 1.
3. For the third row, each element is the sum of the two numbers above it: 1 (1+1) 1, resulting in 1 2 1.
4. This process continues indefinitely.

Pattern in Pascal's Triangle

• First Element: Always 1.
• Last Element: Always 1.
• Middle Elements: Sum of the two numbers above it from the previous row.

Mathematical Representation

Each entry in Pascal’s Triangle corresponds to binomial coefficients:

• The element at the ith row and jth column is denoted as C(i, j) or "i choose j", which is equal to:

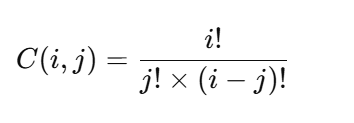
• Where ! denotes factorial.

        1
      1   1
    1   2   1
  1   3   3   1
1   4   6   4   1

• The 0th row is 1.
• The 1st row is 1 1.
• The 2nd row is 1 2 1.
• The 3rd row is 1 3 3 1.
• The 4th row is 1 4 6 4 1.

Note: Row and column are 0 based.

Problem Understanding

Given an integer numRows return the first numRows rows of Pascal's triangle.

In Pascal's triangle:

• The first row has one element with a value of 1.
• Each row has one more element in it than its previous row.
• The value of each element is equal to the sum of the elements directly above it when arranged in a triangle format.

Examples

Example: 1

Input: numRows = 4
Output: [
             [1],
            [1, 1],
           [1, 2, 1],
          [1, 3, 3, 1]
        ]

Explanation: 1st Row has its value set to 1.
All other cells take their value as the sum of the value directly above them.

Example: 2

Input: numRows = 5
Output: [
                 [1],
               [1, 1],
              [1, 2, 1],
             [1, 3, 3, 1],
            [1, 4, 6, 4, 1]
        ]
        
Explanation: 1st Row has its value set to 1.
All other cells take their value as the sum of the values directly above them.

Variations

1️⃣ Variety 1

Problem Statement:

Given the row number r and the column number c, find out the element at position (r , c).

Examples

Example 1:

Input: r = 5, c = 3
Output: 6

Explanation:
         1
       1   1
     1   2   1
   1   3   3   1
 1   4   6   4   1

= (5 - 1)! / (3 - 1)! * (5 - 3)!
= 4! / 2!*2!
= 4 * 3 * 2! / 2!*2!
= 12/ 2
= 6

Example 2:

Input: r = 4, c = 2
Output = 3

Explanation:
        1
      1   1
    1   2   1
  1   3   3   1

= (4 - 1)! / (2 - 1)! * (4 - 2)!
= 3! / 1! * 2!
= 3* 2! / 2!
= 3

Example 3:

Input: r = 1, c = 1
Output: 1

Explanation: The first row only has one element, which is 1.

Intuition:

A brute-force approach to find a specific element in Pascal's Triangle would involve generating the entire triangle up to the given row, then accessing the desired element. While this works, it's inefficient because we compute many unnecessary values when we only need a single element.

We can significantly optimize this by directly computing the combination using the formula:

The idea is to use an optimal formula of nCr to solve this problem.

The element at row r and column c in Pascal's Triangle is:

Element at (r, c) = (r - 1 / c - 1) = (r-1)! / (c-1)! * (r-c)!

Approach:

1. Consider r-1 as n and c-1 as r in the formula of nCr. After that, simply calculate the value of the combination using a loop.
2. Iterate from 0 to r using a variable say i, and in each iteration, multiply (n - i) with the result and divide the result by (i + 1). Finally, the calculated value of the combination will be the answer.

Code:

#include <bits/stdc++.h> 
using namespace std;

class Solution {
public:
    // Function to print the element in rth row and cth column 
    int pascalTriangleI(int r, int c) {
        return nCr(r-1, c-1);
    }
    
private:
    // Function to calculate nCr
    int nCr(int n, int r)  {
        // Choose the smaller value for lesser iterations
        if(r > n-r) r = n-r;
        
        // base case
        if(r == 1) return n;
        
        int res = 1; // to store the result 
        
        // Calculate nCr using iterative method avoiding overflow 
        for (int i = 0; i < r; i++) {
            res = res * (n-i);
            res = res / (i+1);
        }
        
        return res; // return the result 
    }
};

int main() {
    // row number
    int r = 5; 
    // col number
    int c = 3;

    // Create an instance of the Solution class
    Solution sol; 
    
    // Function call to print the element in rth row and cth column 
    int ans = sol.pascalTriangleI(r, c);

    cout << "The element in the rth row and cth column in pascal's triangle is: " << ans;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(C), where C is given column number. For running a loop r times, where R is C - 1.
• Space Complexity: O(1) no extra space used.

2️⃣ Variety 2

Problem Statement

Given the row number n. Print the n-th row of Pascal's triangle.

Intuition:

A naive approach to solve this problem will be to use the formula for the element of rth row and cth column of Pascal's triangle repetitively to find each element in the rth row. The time complexity of this approach will be O(n2) as we need to calculate the value of each element in the nth row.

A better way to solve this is by identifying a pattern in the rows of the Pascal's triangle. The rth row of Pascal's triangle is generated as shown in the figure:

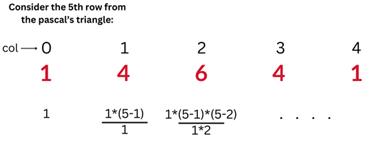
It can be seen that any element in the rth row is of the form:
curr = (prev * (r-i))/(i)
where prev is the previous element in the row and i is the index of the element in the row.

Using this formula, we can generate the rth row of Pascal's triangle in O(n) time complexity

Brute Approach:

1. Iterate over each column (lets say c) from 1 to n and for each column, perform the following steps:
2. Consider n-1 as n and c-1 as r in nCr. After that, simply calculate the value of the combination using a loop.
3. The loop say (i) will run from 0 to r & in each iteration, multiply (n - i) with the result and divide the result by (i + 1). Finally, print the element.
4. Repeat this process for every element of the row.

Brute Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    // Function to calculate nCr (combinations)
    int nCr(int n, int r) {
        long long res = 1;

        // Calculate nCr:
        for (int i = 0; i < r; i++) {
            res = res * (n - i);
            res = res / (i + 1);
        }
        return res;
    }

public:
    /* Function to print Pascal's
    Triangle row for given n*/
    void generate(int n) {
        
        /* Print the entire row of 
        Pascal's Triangle for row n:*/
        for (int c = 1; c <= n; c++) {
            cout << nCr(n - 1, c - 1) << " ";
        }
        
        cout << endl;
    }
};

int main() {
    int n = 5; 

    // Create an instance of the Solution class
    Solution sol; 

    // Print Pascal's Triangle row for row n
    sol.generate(n);

    return 0;
}

Complexity Analysis:

• Time Complexity: O(r * c)
  • Where r is the given row number, and c is the given column index.
• Space Complexity: O(1)

Better Approach:

1. Initialize the list with a size equal to the given row number.
2. Set the first element of the row to 1, as the first element in every row of Pascal's Triangle is always 1.
3. Iterate through the row to compute each value using the above formula.
4. Return the computed row as the final result.

Better Approach Code:

class Solution {
public:
    vector<int> pascalTriangleII(int r) {
        vector<int> result;  // Stores the result row of Pascal's Triangle
        
        result.push_back(1); // First element is always 1
        
        int ans = 1; // Variable to compute each element iteratively

        // Loop to compute the next elements of the row using nCr formula
        for (int col = 1; col < r; col++) {
            // Compute the next binomial coefficient using iterative formula:
            // nCr = (nCr-1 * (n - col)) / col
            ans = ans * (r - col);  
            ans = ans / col;

            // Store the computed value in the result vector
            result.push_back(ans);
        }

        // Return the computed Pascal's Triangle row
        return result;
    }
};

Complexity Analysis:

• Time Complexity:O(R), where R is the given row number.
  • A simple loop is used that runs R times and performs constant time operations in each iteration resulting in a linear time complexity.
• Space Complexity:O(1), as no extra space is used.
  • Note that if the space used to return the row is considered, the space complexity will be O(R) as the space used to store the row is proportional to the row number.

3️⃣ Variety 3

Problem Statement:

Given the row number, print the Pascal's triangle till the row number.

LeetCode:

• https://leetcode.com/problems/pascals-triangle/

Intuition:

A naive way to solve this problem will be to calculate the element n and c (where n is the given row number and c is the column number that will vary from 1 to n) for every column from 1 to n and for every row, using the process used in Pascal Triangle-I. However, this will result in a O(3) time complexity.

A better way to solve this problem will be to generate every row from 1 to n using the method discussed in Pascal Triangle-II and store the entire Pascal's Triangle in a 2D list. Once the entire Pascal's Triangle is generated, we can return the triangle.

Approach:

1. Create a 2D list to hold the values of Pascal's Triangle.
2. For each row i from 0 to n-1, create a list to hold the values of the current row.
3. Generate the row i using the method discussed in Pascal's triangle-II.
4. Append the current row to the triangle. Once all rows are computed, return the triangle.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to generate a single
    row of Pascal's Triangle*/
    vector<int> generateRow(int row) {
        
        long long ans = 1;
        vector<int> ansRow;
        /// Inserting the 1st element
        ansRow.push_back(1); 

        // Calculate the rest of the elements
        for (int col = 1; col < row; col++) {
            ans = ans * (row - col);
            ans = ans / col;
            ansRow.push_back(ans);
        }
        return ansRow;
    }

public:
    /* Function to generate Pascal's
    Triangle up to n rows*/
    vector<vector<int>> generate(int n) {
        vector<vector<int>> pascalTriangle;

        // Store the entire Pascal's Triangle
        for (int row = 1; row <= n; row++) {
            pascalTriangle.push_back(generateRow(row));
        }
        
        //return the pascalTriangle
        return pascalTriangle;
    }
};

int main() {
    int n = 5;
    Solution sol;

    // Generate Pascal's Triangle with n rows
    vector<vector<int>> pascalTriangle = sol.generate(n);

    // Output the Pascal's Triangle
    for (auto& row : pascalTriangle) {
        for (auto& element : row) {
            cout << element << " ";
        }
        cout << endl;
    }

    return 0;
}

OR:

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        // Step 1: Initialize a 2D vector `triangle` with `numRows` rows
        vector<vector<int>> triangle(numRows);

        // Step 2: Iterate over each row from 0 to numRows - 1
        for (int i = 0; i < numRows; i++) {

            // Step 2.1: Create a row of size (i + 1) filled with 1s
            // The first and last elements of a Pascal row are always 1
            vector<int> row(i + 1, 1);

            // Step 2.2: Fill in the middle elements (from index 1 to i - 1)
            // Each element is the sum of the two numbers directly above it
            for (int j = 1; j < i; j++) {
                row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j];
            }

            // Step 2.3: Assign the generated row to the triangle at index i
            triangle[i] = row;
        }

        // Step 3: Return the complete Pascal's Triangle
        return triangle;
    }
};

Complexity Analysis:

• Time Complexity: O(N^2), generating each row takes linear time relative to its size, and there are N rows, leading to a total time complexity of O(N^2).
• Space Complexity: O(N^2), storing the entire Pascal's Triangle requires space proportional to the sum of the first N natural numbers, resulting in O(N^2) space complexity.