Problem Statement

Given an integer array nums of size n. Return the maximum sum possible using the elements of nums such that no two elements taken are adjacent in nums.

A subsequence of array is a sequence that can be derived from the array by deleting some or no elements without changing the order of the remaining elements.

Examples

Example 1:

Input: nums = [1, 2, 4]
Output: 5

Explanation: [1, , 4], these elements are taken to get the maximum sum.

Example 2:

Input: nums = [2, 1, 4, 9]
Output: 11

Explanation: [2, , , 9], these elements are taken to get the maximum sum.

Different Approaches

Recursive Relation:

There are two options:

• Take current element.
  • If it is selected, it means we can't take previous i - 1 but can take i - 2.
• Don't take current element.
  • If it selected, then we can take previous element i - 1.

1️⃣ Recursion

As discussed in the previous problems that recursion can be used when the problem is asking for minimum/maximum of something. Here in this problem it is asking for maximum sum of subsequences, one approach that comes to our mind is to generate all subsequences and pick the one with the maximum sum.

       +-----+-----+-----+-----+-----+
nums = |  1  |  5  |  2  |  1  |  6  |
       +-----+-----+-----+-----+-----+
          0     1     2     3     4
          
Maximum sum of non-adjacent elements = 5 + 6 = 11

To generate all the subsequences, we can use the pick/non-pick technique. This technique can be briefly explained as follows:

• At every index of the array, we have two options:
  • First, to pick the array element at that index and consider it in our subsequence.
  • Second, to leave the array element at that index and not to consider it in our subsequence.

Now, we will try to form the recursive solution to the problem with the pick/non-pick technique. There is one more catch, the problem wants us to have only non-adjacent elements of the array in the subsequence, therefore we need to address that too. In order to do that, while moving ahead, we can keep a track if we took the last index or not.

Steps to form recursive solution:

1. Represent the function in terms of indices: We are given an array which can be easily thought of in terms of indices, at each index an element will be present. f(n-1) will return the maximum sum from 0th index till (n-1)th index. We need to return f(n-1) as our final answer.
2. Try all the choices to reach the goal: As mentioned earlier we will use the pick/non-pick technique to generate all subsequences. In addition to that only pick up the non-adjacent elements in this step.

There are two possible choices that can be made for each index. If we pick an element then, pick = arr[ind] + f(ind-2). The reason we are doing f(ind-2) is because we have picked the current index(ind) element so we need to pick a non-adjacent element so we choose the index ‘ind-2’ instead of ‘ind-1’.

The other choice can be to ignore the current element at index(ind) in our subsequence. So nonPick= 0 + f(ind-1). As we don’t pick the current element, we can consider the adjacent element in the subsequence.

/*It is pseudocode and it is not tied to 
any specific programming language*/
f(ind, arr[]){
    //base condition
    pick = arr[ind] + find(ind-2, arr)
    notPick = 0 + f(ind-1, arr)
}

• Take the maximum of all the choices: As the problem statement asks to find the maximum sum, return the maximum of two choices made in the above step.

/*It is pseudocode and it is not tied to
 any specific programming language*/
f(ind, arr[]){
    //base condition
    pick = arr[ind] + f(ind-2, arr)
    notPick = 0 + f(ind - 1, arr)
    return max(pick, notPick)
}

• Base Conditions:
  • If ind=0, then we know to reach at index=0, we would have ignored the element at index = 1. Therefore, we can simply return the value of arr[ind] and consider it in the subsequence.
  • If ind<0, this case can hit when we call f(ind-2) at ind=1. In this case we want to return to the calling function so we simply return 0 so that nothing is added to the subsequence sum.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Function to solve the problem using recursion
    int func(int ind, vector<int>& arr) {
    // Base cases
    if (ind == 0) 
        return arr[ind];
    if (ind < 0)  
        return 0;

    // Choosing the current element
    int pick = arr[ind] + func(ind - 2, arr);  
    
    // Skipping the current element
    int nonPick = 0 + func(ind - 1, arr);  

    // Return the maximum 
    return max(pick, nonPick);
}
public:
    /*Function to calculate the maximum
    sum of nonAdjacent elements d*/
    int nonAdjacent(vector<int>& nums) {
        int ind = nums.size()-1;
        
        //Return the maximum sum
        return func(ind, nums);
    }
};

int main() {
    vector<int> arr{2, 1, 4, 9};
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the solve function and print the result
    cout << sol.nonAdjacent(arr);

    return 0;
}

Complexity Analysis:

• Time Complexity: O(2 ^ n), where n is the given size of array. This is because each call branches into two more calls, leading to an exponential growth in the number of calls.
  • Since there are n indices, the recursion creates a binary tree of calls, where each node has 2 branches (pick or non-pick);
  • The total number of calls grows exponentially, resulting in O(2 ^ n) calls in the worst case.
• Space Complexity: The space complexity of this recursive approach is O(n). This is because the maximum depth of the recursion stack can go up to n, due to the linear nature of the stack usage relative to the input size n.

2️⃣ Memoization

If we observe the recursion tree, we will observe a number of overlapping subproblems. Therefore the recursive solution can be memoized to reduce the time complexity.

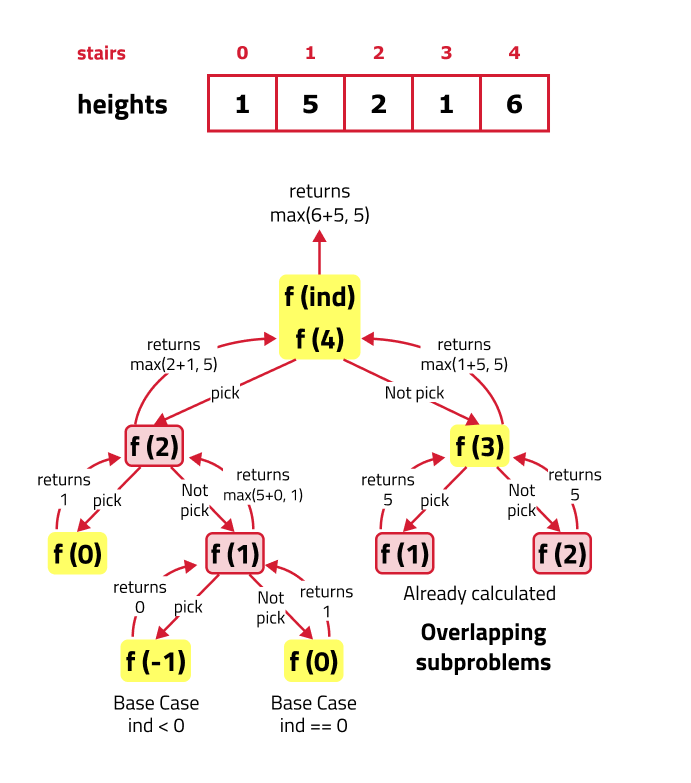
Steps to convert Recursive code to memoization solution:

1. Declare an Array dp[] of Size n: Here, n is the size of the given array in the problem, as the highest number of subproblems can be n(including 0 as well). It represents the solution to the subproblem for any given index. Initially, fill the array with -1, to indicate that no subproblem has been solved yet.
2. While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
3. Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    // Function to solve the problem using memoization
    int func(int ind, vector<int> &arr, vector<int> &dp) {
    // Base cases
    if (ind == 0) 
        return arr[ind];
    if (ind < 0)  
        return 0;
    
    if(dp[ind] != -1){
        return dp[ind];
    }
    // Choosing the current element
    int pick = arr[ind] + func(ind - 2, arr, dp);  
    
    // Skipping the current element
    int nonPick = 0 + func(ind - 1, arr, dp);  

    /* Store the result in dp 
    array and return the maximum */
    return dp[ind] = max(pick, nonPick);
}
public:
    /*Function to calculate the maximum
    sum of nonAdjacent elements d*/
    int nonAdjacent(vector<int>& nums) {
        int ind = nums.size()-1;
        
        //Initialize the dp array with -1
        vector<int> dp(ind+1, -1);
        
        //Return the maximum sum
        return func(ind, nums, dp);
    }
};

int main() {
    vector<int> arr{2, 1, 4, 9};
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the solve function and print the result
    cout << sol.nonAdjacent(arr);

    return 0;
}

Complexity Analysis:

• Time Complexity: O(n), where n is the given size of array. The overlapping subproblems will return the answer in constant time O(1). As total subproblems can be at max N. Therefore it will take O(N).
  • The initialization of vector takes O(n).
  • With memoization, each subproblem is computed only once. After computing the result for an index ind, the value is stored in the dp array, ensuring that no recursive call is made for the same index multiple times. So it takes O(n).
• Space Complexity: O(N) + O(N), As stack space of O(N) and an dp array O(N) is used. Therefore total space complexity will be O(N) + O(N) ≈ O(N).

3️⃣ Tabulation

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

1. Declare an Array dp[] of Size n: Here, n is the size of the array provided as input. It represents the solution to the subproblem for any given index.
2. Setting Base Cases in the Array: In the recursive code, we knew the answer for base case, when 'ind' = 0, Here, dp[0] is initialized directly to arr[0] because if there is only one element in the array, that element itself is the maximum sum.
3. Iterative Computation Using a Loop: Set an iterative loop that traverses the array( from index 1 to n-1). To compute the solution for larger values, use a loop that iterates from the smallest subproblem up to n-1.
4. Explanation of dp[i] Calculation: The current value(dp[i]) represents the subproblem and by the recurrence relation it is obvious that dp[i] is calculated by either picking the current element or not picking it (dp[i-2] + arr[i] and dp[i-1]))
5. Choosing the maximum: Update dp[i] to store the maximum of these two values pick and nonPick.
6. Returning the last element: The last element of the dp array is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.

Code:

int nonAdjacent(vector<int>& nums) {
    // Check for edge cases:
    // If the input vector is empty, the maximum sum is 0.
    if (nums.empty()) return 0;

    // If there is only one element in the input vector,
    // the maximum sum is the value of that single element.
    if (nums.size() == 1) return nums[0];

    // Create a DP array to store the maximum sum at each index.
    // dp[i] will represent the maximum sum of non-adjacent elements
    // from the start of the array up to index `i`.
    vector<int> dp(nums.size(), 0);

    // Base case:
    // The maximum sum at index 0 is simply the value of the first element.
    dp[0] = nums[0];

    // Fill the DP array for each index starting from 1.
    for (int i = 1; i < nums.size(); i++) {
        // Option 1: Include the current element `nums[i]`.
        // If we include `nums[i]`, we cannot include the previous element `nums[i-1]`.
        // Instead, we add `nums[i]` to the maximum sum up to index `i-2`.
        // If `i-2` is out of bounds (i.e., `i < 2`), we add 0.
        int pick = nums[i] + ((i - 2) < 0 ? 0 : dp[i - 2]);

        // Option 2: Exclude the current element `nums[i]`.
        // If we don't include `nums[i]`, the maximum sum remains the value at `dp[i-1]`.
        int nopick = dp[i - 1];

        // Take the maximum of the two options to get the best sum up to index `i`.
        dp[i] = max(pick, nopick);
    }

    // The last element in the DP array contains the maximum sum of non-adjacent elements
    // for the entire array.
    return dp[nums.size() - 1];
}

Complexity Analysis:

• Time Complexity: O(n), where n is the given size of array. As each element of the array is processed exactly once in a single pass.
• Space Complexity: O(n), as an additional dp array is used, which stores results for each element of the array.

4️⃣ Space Optimization

If we do some observation, we find that the values required at every iteration for dp[i] are dp[i-1] and dp[i-2]. we see that for any i, we do need only the last two values in the array. So is there is no need to maintain a whole array for it.

Let us call dp[i-1] as prev and dp[i-2] as prev2. Now understand the following illustration:

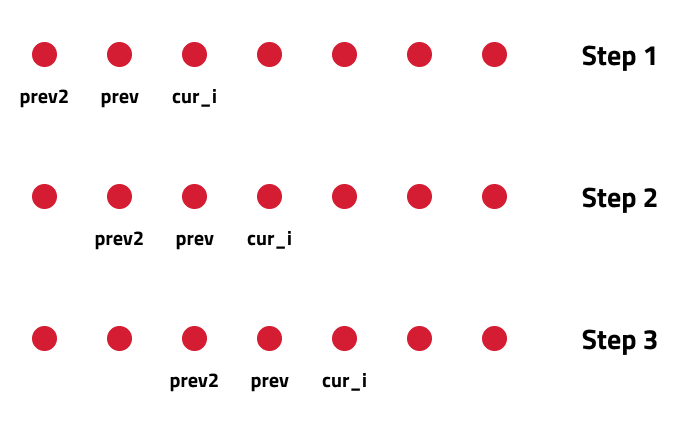
• Each iteration cur_i and prev become the next iteration’s prev and prev2 respectively. Therefore after calculating cur_i, if we update prev and prev2 according to the next step, we will always get the answer.
• After the iterative loop has ended we can simply return prev as our answer. As at the end of the loop prev will contain curr_i, the maximum sum.

Code:

int nonAdjacent(vector<int>& nums) {
    // Edge Case 1: If the input array is empty, the maximum sum is 0.
    if (nums.empty()) return 0;

    // Edge Case 2: If there is only one element in the array,
    // the maximum sum is the value of that single element.
    if (nums.size() == 1) return nums[0];

    // Initialize two variables to keep track of the results for the last two indices:
    // `prev` represents the maximum sum up to the previous index (i-1).
    // `prev2` represents the maximum sum up to the index before the previous one (i-2).
    int prev = nums[0]; // Initially, the maximum sum for the first element is the element itself.
    int prev2 = 0;      // Before the first element, there is no sum, so initialize it to 0.

    // Iterate through the array starting from the second element (index 1).
    for (int i = 1; i < nums.size(); i++) {
        // Option 1: Include the current element `nums[i]`.
        // If we include `nums[i]`, add it to the maximum sum up to index `i-2` (stored in `prev2`).
        int pick = nums[i] + prev2;

        // Option 2: Exclude the current element `nums[i]`.
        // If we don't include `nums[i]`, the maximum sum remains the sum up to index `i-1` (stored in `prev`).
        int nopick = prev;

        // Compute the maximum sum for the current index by choosing the best option.
        int current = max(pick, nopick);

        // Update `prev2` and `prev` for the next iteration:
        // - `prev2` becomes the old `prev` (i.e., the max sum up to index i-1).
        // - `prev` becomes the new `current` (i.e., the max sum up to index i).
        prev2 = prev;
        prev = current;
    }

    // After the loop, `prev` holds the maximum sum for the entire array.
    return prev;
}

Complexity Analysis:

• Time Complexity: O(N), where N is the given size of array. As each element of the array is processed exactly once in a single pass.
• Space Complexity: O(1), as there is no extra space used.