Problem Statement

Given an array nums, return the kth largest element in the array.

Examples

Example 1:

Input: nums = [4, 3, 2, 1], k = 2
Output: 3

Example 2:

Input: nums = [-5, 3, 1, -2], k = 4
Output: -5

Example 3:

Input: nums = [5, 3, 4, 4], k = 3
Output: 4

Different Approaches

1️⃣ Brute Force Approach

Intuition:

Sort the entire array and then directly access the kth largest element.

Approach:

1. Sort the array in ascending order.
2. The kth largest element is at index n - k (using 0-based indexing).

Code:

int kthLargestBruteForce(vector<int>& arr, int k) {
    sort(arr.begin(), arr.end());
    return arr[arr.size() - k];
}

Complexity Analysis:

• Time Complexity:O(n log n)
  • Due to sorting.
• Space Complexity:O(1)
  • If done in-place, otherwise extra space for the sorted array.

2️⃣ Min-Heap Approach

Intuition:

A complete naive approach would be to sort the array and return the kth element from the end. This would take O(N*logN) time due to sorting the array.

The problem is efficiently solved by leveraging the properties of a min-heap. Since only the K largest elements matter, a min-heap of size K is maintained. While processing any element, it is checked if it is among the K largest elements encountered so far. If it is, the smallest element is removed from the min-heap and the new element is inserted.

Algorithm:

1. A min-heap of size K is maintained to store the K largest elements encountered so far.
2. The first K elements from the input are inserted into the min-heap.
3. For each remaining element, if it is greater than the smallest element in the heap, the smallest element is removed, and the new element is inserted.
4. After processing all elements, the top of the min-heap contains the Kth largest element, which is returned.

Code:

 class Solution {
public:
    int kthLargestElement(vector<int>& nums, int k) {
        // Create a min-heap (priority_queue with greater comparator)
        // The min-heap will store the k largest elements seen so far.
        priority_queue<int, vector<int>, greater<int>> pq;

        // Iterate over each number in the input vector
        for (auto num : nums) {
            // Push the current number into the min-heap
            pq.push(num);
            
            // If the size of the heap exceeds k, 
            // remove the smallest element so that only the k largest remain.
            if (pq.size() > k) {
                pq.pop();
            }
        }
        
        // The top of the min-heap is the kth largest element
        return pq.top();
    }
};

Complexity Analysis:

• Time Complexity:O(n log k), where n is the size of the given input array.
  • Traversing the array takes O(n) time and for each element, in the worst case, we perform heap operations which takes O(log k) time.
  • Note that k can be equal to N in the worst case, making the worst-case time complexity as O(n log n).
• Space Complexity:O(k)
  • As a Min-heap data structure of size k is used to store the k largest elements.

3️⃣ Quick Select

Intuition:

The earlier approach was taking a worst-case time complexity of O(N*LogN) which is not efficient. This hints to solve the problem in O(N) time complexity. The key idea will be to use the logic in Quick-sort.

In Quick-sort, if the aim is to sort the array in non-increasing order, a pivot element is chosen randomly and the array is partitioned such that all elements greater than the pivot belong to the left portion and all elements smaller than or equal to the pivot belongs to the right portion with the pivot separating the two portions. Refer to the image below for better understanding:

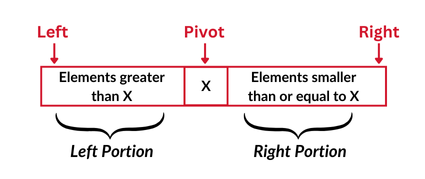
Note that the pivot element will be the Kth largest element when the size of the left portion of the array is K-1. This is because the left portion contains K-1 elements greater than the pivot element.

Thus, if the pivot element is at its correct position, return the element. If the pivot element is smaller than the kth element, search the right side of the pivot. Otherwise, search the left side of the pivot.

Approach:

1. A random index within the current search range is chosen as the pivot to reduce the risk of worst-case time complexity.
2. Partition Around the Pivot:
   1. The pivot element is swapped with the leftmost element to simplify the partitioning process.
   2. Elements greater than the pivot are moved to the left portion of the array.
   3. Elements smaller than or equal to the pivot remain in the right portion.
   4. The pivot is then placed in its correct position, ensuring all larger elements are on its left and all smaller ones on its right.
3. If the pivot index matches k-1, the element at this index is the Kth largest and is returned as the answer.
4. If the pivot index is greater than k-1, the search continues in the left portion of the array. Otherwise, the search takes place for the right portion of the array.
5. The process continues until the Kth largest element is found.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to get the Kth largest element 
    int kthLargestElement(vector<int>& nums, int k) {
        // Return -1, if the Kth largest element does not exist
        if(k > nums.size()) return -1;
        
        // Pointers to mark the part of working array 
        int left = 0, right = nums.size() - 1;
        
        // Until the Kth largest element is found
        while(true) {
            // Get the pivot index
            int pivotIndex = randomIndex(left, right);
            
            // Update the pivotIndex
            pivotIndex = partitionAndReturnIndex(nums, pivotIndex, left, right);
            
            // If Kth largest element is found, return
            if(pivotIndex == k-1) return nums[pivotIndex];
            
            // Else adjust the end pointers in array 
            else if(pivotIndex > k-1) right = pivotIndex - 1;
            else left = pivotIndex + 1;
        }
        
        return -1;
    }
    
private:
    // Function to get a random index 
    int randomIndex(int &left, int &right) {
        // length of the array 
        int len = right - left + 1;
        
        // Return a random index from the array 
        return (rand() % len) + left;
    }
    
    // Function to perform the partition and return the updated index of pivot
    int partitionAndReturnIndex(vector<int> &nums, int pivotIndex, int left, int right) {
        int pivot = nums[pivotIndex]; // Get the pivot element
        
        // Swap the pivot with the left element
        swap(nums[left], nums[pivotIndex]);
        
        int ind = left + 1; // Index to mark the start of right portion
        
        // Traverse on the array 
        for(int i = left + 1; i <= right; i++) {
            
            // If the current element is greater than the pivot
            if(nums[i] > pivot) {
                // Place the current element in the left portion
                swap(nums[ind], nums[i]);
                
                // Move the right portion index
                ind++;
            }
        }
        
        swap(nums[left], nums[ind-1]); // Place the pivot at the correct index
        
        return ind-1; // Return the index of pivot now
    }
};


// Driver code
int main() {
    vector<int> nums = {-5, 4, 1, 2, -3};
    int k = 5;

    // Creating an object of the Solution class
    Solution sol;

    // Function call to get the Kth largest element 
    int ans = sol.kthLargestElement(nums, k);

    // Output array
    cout << "The Kth largest element in the array is: " << ans << endl;

    return 0;
}

#include <iostream>
#include <vector>
#include <cstdlib> // For rand()
using namespace std;

// Partition function to rearrange the array
// It places the pivot at its correct position in sorted order
// Elements greater than pivot are placed on the left, smaller ones on the right
int partition(vector<int>& nums, int left, int right) {
    int pivot = nums[right]; // Choosing the rightmost element as pivot
    int i = left;  // Pointer for placing elements greater than pivot

    for (int j = left; j < right; j++) {
        if (nums[j] >= pivot) { // Ensuring larger elements come first
            swap(nums[i], nums[j]);
            i++; // Move pointer to the next position
        }
    }
    swap(nums[i], nums[right]); // Place pivot at its correct position
    return i; // Return the pivot index
}

// QuickSelect function to find the Kth largest element
int quickSelect(vector<int>& nums, int left, int right, int k) {
    if (left == right) return nums[left]; // Base case: only one element

    int pivotIndex = partition(nums, left, right); // Partition the array

    if (pivotIndex == k) {
        return nums[pivotIndex]; // Found the Kth largest element
    } else if (pivotIndex < k) {
        return quickSelect(nums, pivotIndex + 1, right, k); // Search right part
    } else {
        return quickSelect(nums, left, pivotIndex - 1, k); // Search left part
    }
}

// Function to find the Kth largest element in the array
int findKthLargest(vector<int>& nums, int k) {
    int n = nums.size();
    return quickSelect(nums, 0, n - 1, k - 1); // Convert K to 0-based index
}

int main() {
    vector<int> arr = {3, 2, 1, 5, 6, 4};
    int k = 2;

    cout << "The " << k << "th largest element is: " << findKthLargest(arr, k) << endl;
    return 0;
}

Complexity Analysis:

• Time Complexity:O(N), where N is the size of the given array.
  • In the average case (when the pivot is chosen randomly):
    • Assuming the array gets divided into two equal parts, with every partitioning step, the search range is reduced by half. Thus, the time complexity is O(N + N/2 + N/4 + ... + 1) = O(N).
  • In the worst-case scenario (when the element at the left or right index are chosen as pivot):
    • In such cases, the array is divided into two unequal halves, and the search range is reduced by one element with every partitioning step. Thus, the time complexity is O(N + N-1 + N-2 + ... + 1) = O(N2). However, the probability of this worst-case scenario is negligible.
• Space Complexity:O(1), as we are modifying the input array in place and using only a constant amount of extra space.