Variant 1:

Problem Statement

Given an integer array coins[] of size N, which represents different denominations of coins, and an integer sum, the task is to find the number of possible combinations to make the given sum using the coins. You have an infinite supply of each type of coin, meaning each coin can be used any number of times.

Examples:

Examle 1:

Input: coins[] = {1, 2, 3}, sum = 4
Output: 4

Explanation:
The possible combination are:
1) {1, 1, 1, 1}
2) {1, 1, 2}
3) {2, 2}
4) {1, 3}

Example 2:

Input: coins[] = {2, 5, 3, 6}, sum = 10
Output: 5

Explanation;
The possible combinations are:
1) {2, 2, 2, 2, 2}
2) {2, 2, 3, 3}
3) {2, 2, 6}
4) {5, 5}
5) {5, 3, 2}

Different Approaches

1️⃣ Recursive Approach

The recursive approach tries to break the problem into smaller subproblems by considering two possibilities for each coin:

1. Include the coin: Subtract the coin value from the sum and try to make the remaining sum with the same set of coins.
2. Exclude the coin: Skip the current coin and try to make the same sum with the remaining coins.

This approach generates all possible combinations of coins by making decisions at each step to either include or exclude a coin.

Recursive Formula:

Let count(coins, index, size, sum) be the number of ways to make sum using the first n coins.

count(coins, index, size, sum) = count(coins, index, size, sum - coins[index-1]) + count(coins, index - 1, sum)

Where:

• count(coins, index, sum - coins[index]): Case where the current coin is included.
• count(coins, index+1, sum): Case where the current coin is excluded.

Base Cases:

1. If sum == 0: There's exactly 1 way to make the sum 0 (by choosing no coins).
2. If sum < 0: No solution is possible, return 0. Because sum become negative.
3. If index == size: No coins are left but the sum is still positive, return 0.

Dry Run:

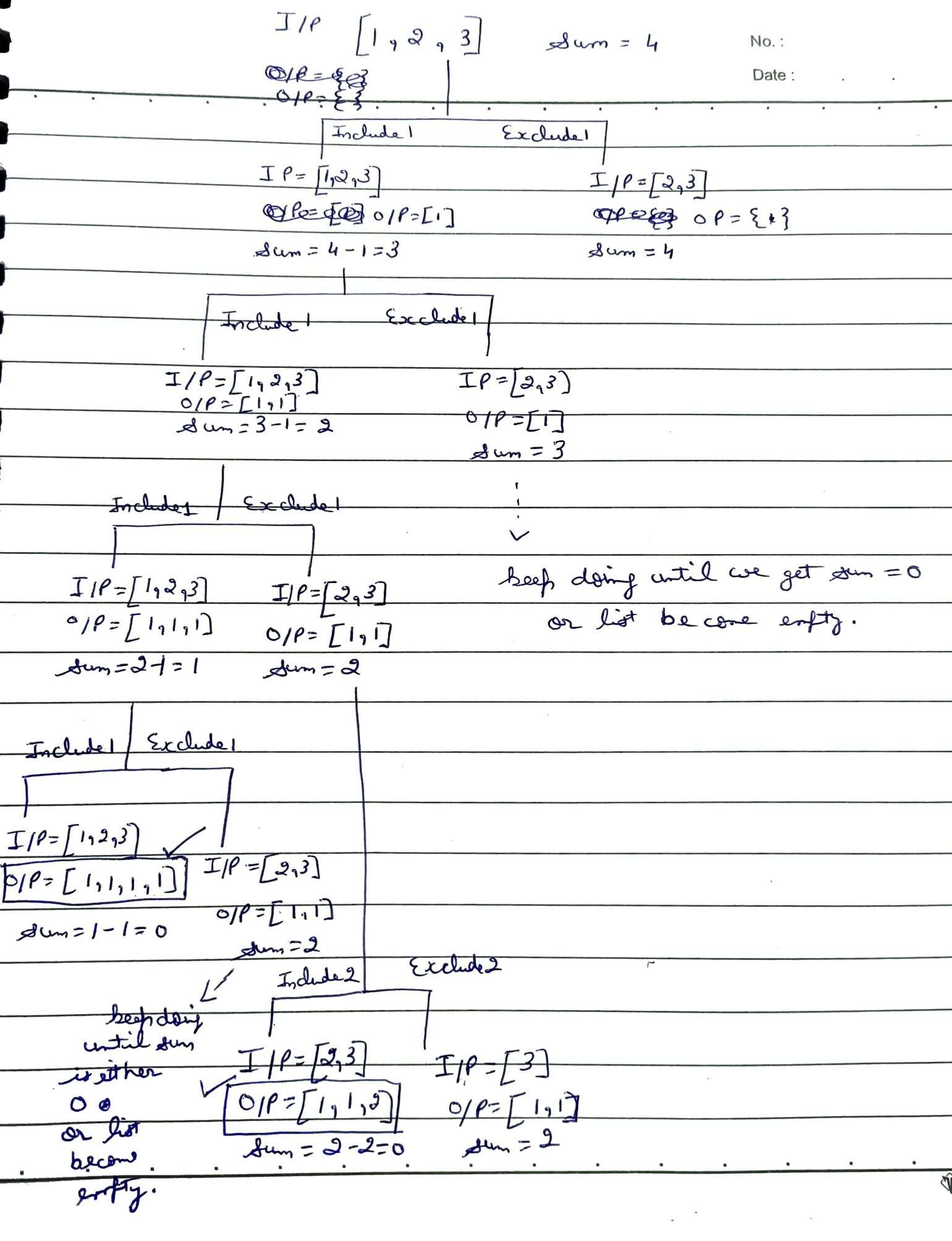
Code:

#include <iostream>
#include <vector>

using namespace std;

int countWays(vector<int>& coins, int index, int size, int sum) {
    // Base case: If the sum is 0, return 1 (there is 1 way to make sum 0)
    if (sum == 0)
        return 1;
    
    // If the sum is less than 0, return 0 (no solution exists)
    if (sum < 0)
        return 0;
    
    // If no coins are left and sum is still greater than 0, return 0 (no solution)
    if (index == size)
        return 0;
    
    // Count the ways by including the current coin
    int intake = countWays(coins, index, size, sum - coins[index]);
    
    // and excluding it.
    int exclude = countWays(coins, index + 1, size, sum);
    return intake + exclude;
}


int main()
{
    vector<int> coins = {1, 2, 3};
    int sum = 4;

    cout<< countWays(coins, 0, coins.size(), sum);
    
   
}

Explanation:

1. Base Cases:
   • If the sum is exactly 0, the function returns 1, as there's exactly one way to make the sum 0 (by choosing no coins).
   • If the sum becomes less than 0, the function returns 0, because you can't achieve a negative sum.
   • If you've exhausted all coins (i.e., index == size) and still haven't reached the target sum, the function returns 0, indicating that no solution exists for the current combination of coins.
2. Recursive Logic:
   • Include the current coin: This reduces the sum by the value of the current coin (sum - coins[index]) and keeps the index at the same position, since you can use the same coin multiple times.
   • Exclude the current coin: This moves to the next coin (index + 1) without reducing the sum.
3. Final Answer:
   • The total number of ways to make the sum is the sum of these two possibilities (including and excluding the current coin).

Complexity Analysis:

• Time Complexity: O(2^n), where n is the number of coins (elements) in the array.
• Space Complexity: O(n), where n is the number of coins (elements) in the array.