Constraints as Clues: A Guide to Efficient DSA Problem Solving

When solving problems in Data Structures and Algorithms (DSA), constraints serve as a guide to select the most efficient approach. Constraints—provided in the problem description—tell us how large the inputs can be, how fast the algorithm must run, and what kind of data structures or optimizations we might need. Understanding and interpreting these constraints is a valuable skill for any developer.

🧩 What Are Constraints in DSA Problems?

In DSA problems, constraints are rules or limits defined for the input and output. They help us:

• Understand how big the inputs can be
• Choose an efficient algorithm that works within time and memory limits
• Avoid unnecessary brute-force approaches

🔍 Types of Constraints

1️⃣ Input Size Constraints

This tells you how large the input can be, which directly affects the type of algorithm you should consider. A brute-force approach that works for small input sizes may not be feasible for larger ones. It often appears something like n <= 10^5, where n is the number of elements in the input.

• 1 ≤ n ≤ 10^5: The input size (n) can be up to 100,000 elements.
• 1 ≤ T ≤ 100: There can be up to 100 test cases.
• 1 ≤ rows, cols ≤ 1000: For matrix problems, this defines the grid dimensions.

💡 Input size directly impacts the algorithm you choose. For example:

• O(n²) is okay if n ≈ 1000
• O(n log n) is safe if n ≤ 10^5
• O(n) is ideal when n approaches 10^8

2️⃣ Value Range Constraints

These define the possible range of values for each element. For example, a problem might specify that all numbers are between 1 and 1000. This can affect whether you should use certain data structures, like hash maps or arrays, for efficient lookup or computation.

• 1 ≤ arr[i] ≤ 10^6: Each array element is between 1 and 1,000,000.
• -10^9 ≤ x ≤ 10^9: Common in problems involving coordinates or ranges.

These affect:

• Whether to use a hash map or an array for lookups
• Whether integer overflow might occur (use long long in C++ or int64)

3️⃣ Output Constraints

These describe:

• The type and format of the output
• Any precision requirements (especially for floating-point answers)
• The range of acceptable answers.

For example: “Output should be accurate up to 6 decimal places” or “Return -1 if not possible.”

Why is this important?

Because it tells you how much work your code needs to do in the worst case and what kind of algorithms will run within time limits.

⚙️ How Online Coding Platforms Work

When you submit code to platforms like LeetCode, Codeforces, or HackerRank, your solution goes through a multi-step process to evaluate its correctness and efficiency.

Online coding platforms uses a systematic process to evaluate submissions and determine if they pass the test cases.

Each problem has a set of input and expected output files stored behind the hood.

I1, I2, I3, ...In = Input files
EO1, EO2, EO3, ...EOn = Output files with expected output

When we submit the code, it is run against all these input files. This generates a list of generated output file.

GO1, GO2, GO3, ...GOn = Generated Output

The generated output files are compared with the corresponding expected output files. If they match, your solution is correct.

Here's a detailed look at how this process works from submission to result:

1️⃣ Submission and Compilation:

When you submit your solution on the platform, the code is uploaded to the platform's server and typically goes through a compilation phase (if the language requires compilation, such as C++ or Java).

During this phase:

• The platform checks for syntax errors and language-specific compilation errors.
• If the code compiles successfully, it moves to the next phase. If not, the platform returns compilation errors to the user.

2️⃣ Isolation and Sandbox Execution:

To run the code securely and prevent it from affecting other users or the server, platforms often execute code in isolated environments or sandboxes.

Each submission runs in the container or virtual machine with:

• Limited memory, CPU, and execution time.
• Restricted access to the system to avoid security issues (e.g., blocking access to the file system, network, or other processes).

The isolation ensures that even if the code contains infinite loops, malicious instructions, or excessive memory usage, it won't impact the platform's stability.

3️⃣ Loading and Running Test Cases:

Once the code is running in the sandbox, the platform runs it against a series of test cases:

• Public test cases: Some platforms show a basic test cases to the user when they submit. These often include simple cases to help debug syntax and logic errors.
• Hidden test cases: These are usually more complex cases not shown to the user to prevent hardcoding or biased solutions. They include edge cases and large input that test the code's efficiency and robustness.

Each test case is typically provided to the program through standard input and evaluate based on the standard output.

Each problem has a set of:

• Input files: I1, I2, .. In
• Expected output files: EO1, EO2, .., EOn

When your code runs:

• It reads each input (I1, I2, …)
• Produces a corresponding output (GO1, GO2, …)
• Compares your output with expected output (EO1 == GO1, etc.)

4️⃣ Time Limit and Memory Limit Enforcement:

During execution, the platform monitors CPU time and memory usage for each test case:

• Time Limit: Each test case has a maximum execution time (e.g., 1-2 seconds for most cases). If the code takes longer than this limit, it times out (resulting in Time Limit Exceeded (TLE) error).
• Memory Limit: The platform also enforces a memory limit (e.g., 256 MB, 512 MB, or 1 GB). If the code uses more than the allowed memory, it results in a Memory Limit Exceeded (MLE) error.

These limits ensures that inefficient or resource-intensive solutions fail, encouraging uses to optimize their code.

5️⃣ Validation of Output:

For each test case, the platform compares the program's output to the expected output:

• Exact Match: For most problems, the output needs to match exactly.
• Tolerance: For floating-point numbers, a small tolerance range (epsilon) is often allowed due to precision issues.
• Output Format: Some platforms require the output to match a specified format strictly, so even extra spaces or line breaks may cause the output to fail validation.

If the output matches the expected result for a test case, that test case is marked as passed. Otherwise, it fails with an Incorrect Answer (WA) error.

6️⃣ Handling Edge Cases and Large Inputs

• Platforms typically include test cases that cover a variety of scenarios:
  • Basic cases: Simple inputs to check the general logic of the code.
  • Edge cases: Unusual or extreme cases, such as empty inputs, maximum constraints, or cases that require special handling.
  • Stress test cases: These involve large inputs near the upper limit of constraints to check the efficiency and performance of the solution.
• Edge cases help catch common mistakes, such as division by zero, handling of empty inputs, and off-by-one errors, while large inputs ensure the code meets the efficiency requirements of the problem.

7️⃣ Result Compilation and Feedback:

After running all test cases,  the platform compiles the result:

• If the code passes all test cases, the submission is marked as Accepted.
• If any test case fails, the platform displays the type of error (e.g., TLE, MLE, WA, etc.) and may provide feedback on which test cases failed. However, hidden test cases usually don’t reveal detailed output to prevent reverse-engineering of the solution.

Some platforms show partial results if only a subset of test cases pass, along with the score associated with those cases.

8️⃣ Scoring and Ranking (if applicable)

• If the problem is part of a contest or a scored assignment, the platform calculates the score based on the number of test cases passed and potentially the efficiency of the solution.
• For competitive platforms, the score might be affected by factors like the time taken to submit a solution, the number of incorrect attempts, or other metrics relevant to the contest.

Summary of the Process

🤔 Why Constraints are given in the Coding Problems

1️⃣ Testing the Developer's Problem-Solving and Optimization Skills

• Algorithm Choice and Optimization: Constraints help determine whether a developer can choose the right algorithm based on the input size. For example, if a problem allows n to go up to 10^5, the developer should be able to recognize that a brute-force won't work and instead apply a more efficient algorithm.
• Edge Case Handling: Constraints encourage developers to handle edge cases effectively. For instance, if n >= 1, it suggests that the code should handle small input gracefully, such as an array with a single element.
• Efficient Data Structures: Constraints challenge developers to choose appropriate data structures. For example, large constraints might necessitate using a hash map for O(1) lookups rather than a list that requires O(n) searches.

Overall, constraints push developers to consider the problem’s complexity and improve their problem-solving skills by choosing the right tools and methods.

2️⃣ Enforcing Time Limits for Code Efficiency

• Ensuring Feasible Execution Time: Constraints ensure that the solution will run within the platform’s execution limits (often 1-2 seconds per test case). If the constraints allow large values, developers must use efficient solutions to avoid a Time Limit Exceeded (TLE) error.
• Avoiding Inefficient Code: Without constraints, developers might write slow, brute-force solutions that pass for small inputs but fail on large ones. Constraints discourage inefficient code by setting limits that only optimized solutions can satisfy.
• Memory Management: Constraints also help enforce memory limits by specifying input ranges that require developers to consider memory efficiency, avoiding data structures or solutions that consume too much memory.

3️⃣ Setting a Fair Benchmark for Evaluation

• Constraints create a standardized challenge for all developers, ensuring that only well-optimized code passes all test cases. This levels the playing field in competitive programming and allows for fair scoring, as only those who can manage time and space complexity within the constraints will succeed.
• They serve as a benchmark to distinguish between solutions that are merely correct and those that are efficient and optimized, rewarding developers who achieve both.

🖥 Server Speed Assumption:

Most coding platforms assume that their server can handle about 10^8 operations per second. This estimation helps set a practical standard for time limits on problems and serves as a benchmark for developers to gauge the efficiency of their solutions.

• Coding platforms often impose a time limit of 1-2 seconds per test case.
• Assuming 10^8 operations per second, this allows around 10^8 to 2*10^8 operations in  the allotted time.
• Although actual hardware varies, the 10^8 operations per second benchmark provides a consistent guideline that works well across platforms, allowing developers to make reasonable assumption about time limits when planning their solutions.

While the actual computation power may be higher, the 10^8 operations per second estimate is a useful benchmark.

• If time limit = 1 sec -> you have ~10^8 operations
• Use this to estimate the feasilbility of your algorithm:
  • O(n^2) works only if n ~ 10^3
  • O(n log n) works if n ~ 10^5 to 10^6
  • O(n) works for n ~ 10^7 to 10^8

Types of Constraints

1️⃣ Input Size Constraints

These constraints specify the size of the input data, such as the number of elements in an array, the length of a string, or the number of test cases.

• Array Length / List Size: For example, n ≤ 10^5 means that the array or list can contain up to 100,000 elements.
• Number of Test Cases: If a problem involves multiple test cases, you may see constraints like T ≤ 100, indicating that up to 100 test cases may be provided.
• Dimensions in Matrix Problems: For problems involving matrices, constraints like 1 ≤ rows, columns ≤ 1000 specify the maximum possible matrix size.

2️⃣ Value Range Constraints

These constraints indicate the range of values that elements can take within the input structures (like arrays, matrices, or strings).

• Element Value Ranges: You might see constraints like 1 ≤ arr[i] ≤ 10^6, which define the minimum and maximum values that each element in an array can hold.
• String Characters and Length: For example, constraints like 1 ≤ |S| ≤ 10^5 specify the maximum string length, and if the problem mentions that S contains only lowercase letters, you don’t have to handle uppercase letters or other characters.
• Limits on Numerical Inputs: For integer inputs, constraints like 0 ≤ x ≤ 10^9 indicate the allowed range of values for a number. If values can be negative, this will also be mentioned, such as -10^6 ≤ x ≤ 10^6.

3️⃣ Output Constraints

Output constraints specify requirements for the solution's format or precision.

• Precision for Floating-Point Outputs: If a problem involves decimal values, it might specify an output precision like “output the result rounded to two decimal places” or |answer - expected_answer| < 10^-6 to indicate acceptable precision tolerance.
• Output Range and Formatting: If a problem requires a boolean answer (e.g., "YES" or "NO"), it will often mention acceptable responses. Similarly, problems involving large numbers might specify that the output should be modulo some number (e.g., output % 10^9 + 7).

4️⃣ Special Constraints

Some problems come with additional constraints or conditions that influence your approach.

• Uniqueness or Sorted Order: A problem might state that array elements are unique, meaning you don’t need to handle duplicates. Alternatively, if the array is sorted, you can use efficient techniques like binary search.
• Graph Constraints: In graph problems, constraints might specify properties like a graph being acyclic, connected, or undirected. These properties can help narrow down which graph algorithms to use (e.g., BFS/DFS for connected graphs or topological sort for directed acyclic graphs).
• Range of Queries: If a problem involves a high number of queries, the constraints might limit the range of each query (e.g., 1 ≤ L, R ≤ n). This can indicate whether solutions should involve preprocessing or advanced data structures like segment trees or binary indexed trees for efficient query handling.

5️⃣ Edge Case Constraints

Edge case constraints help clarify unusual scenarios that should be handled.

• Empty Input or Single Element Cases: Constraints like 1 ≤ n ≤ 1000 imply that n could be as low as 1, meaning your solution should handle single-element cases gracefully.
• Boundary Values: If a problem involves high numerical limits, like x = 10^9, be prepared to manage potential integer overflow, or consider more efficient approaches if necessary.
• Special Values or Repetitive Elements: Some problems might specify that all elements are identical or that a particular value appears frequently. These conditions might allow for optimization based on early stopping or specialized cases.

⏱️ Time Complexity Estimation From Constraints

When solving DSA problems, constraints often hint at the expected time complexity rather than stating it outright. You need to deduce whether your algorithm can run within the time limit, typically 1 second per test case, based on input size.

Here's a quick cheat sheet to guide your thinking:

🧠 How to Check If Your Algorithm Meets Time Constraints

Below is given the all possible complexities on a graph:

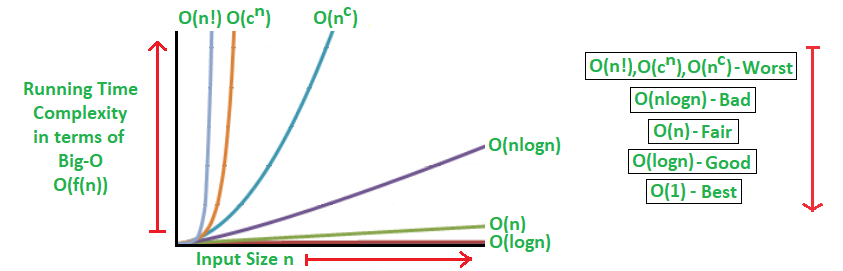
Use the 10^8 operations per second rule:

1. Take the max n constraint from the problem.
2. Apply it to your algorithm’s time complexity expression (n, n log n, n^2, etc.). By replace the n with your value.
3. Estimate the number of operations.
4. Compare it to the 10^8 ops/second benchmark.

If the number of operations is within 10^8, your code is likely to complete within 1 second and pass the time limit. If it's significantly over 10^8, your code may result in a  Time Limit Exceeded (TLE) error, especially if the platform has a strict 1-second limit per test case.

🧪 Step-by-Step Example:

Let's say we have a problem with a constraint: n ≤ 10^5, and your solution has a time complexity of O(n^2).

1. Calculate Operations:

   n^2 = (10^5)^2 = 10^10 operations

2. Compare to the 10^8 Benchmark:

   10^10 operations > 10^8 operations ❌ Too Slow

   This is far above 10^8, meaning your solution will likely exceed the time limit.

3. Conclusion: An O(n^2) solution is too slow for n = 10^5 and may result in TLE. You would need to optimize the algorithm to something like O(n log n) or O(n) to make it feasible.

What About Input Value Ranges?

Sometimes constraints on value ranges help you decide whether:

• You can use counting sort
• You need to worry about integer overflow
• You should use hash maps or prefix sums

Example:

1 <= arr[i] <= 1000

This means you can safely use:

int freq[1001]; // For frequency counting

But if it was 1 <= arr[i] <= 1e9, then you would need a map instead of an array.

📑 Table for Time Constraints

Always check the input size and pick the fastest possible algorithm. Use the below table to avoid TLE (Time Limit Exceeded) in interview or contests.

• O(log n) is super efficient. You can handle values up to 10^18 or more.
• O(n) is suitable up to n ≈ 10^8
• O(n log n) is efficient for n ≤ 10^6
• O(n²) is okay for n ≤ 10^4
• O(n³) starts becoming borderline at n ≈ 500
• O(n⁴) should only be used when n ≤ 90
• O(2^n) and O(n!) are only feasible for small n (usually n ≤ 25 or n ≤ 10 respectively)

💡 Best Practices

• Read constraints before writing code. They tell you what’s possible.
• Use them to plan your algorithm and test for edge cases.
• Benchmark your approach using the 10⁸ rule.
• Watch out for traps like:
  • Missing edge cases (e.g., n = 0, or maximum input)
  • Overflow from large ranges
  • Unhandled precision in floating points

References

• https://codeforces.com/blog/entry/21344
• http://aurabhkurve/predicting-dsa-solutions-using-constraints-4jnf