Problem Statement
Given two sorted arrays a and b of size m and n respectively. Find the kth element of the final sorted array.
Examples
Example 1:
Input: a = [2, 3, 6, 7, 9], b = [1, 4, 8, 10], k = 5
Output: 6
Explanation: The final sorted array would be:
[1, 2, 3, 4, 6, 7, 8, 9, 10]
The 5th element of this array is 6.Example 2:
Input: a = [100, 112, 256, 349, 770], b = [72, 86, 113, 119, 265, 445, 892], k = 7
Output: 256
Explanation: The final sorted array would be:
[72, 86, 100, 112, 113, 119, 256, 265, 349, 445, 770, 892]
The 7th element is 256.Example 3:
Input: a = [2, 3, 6], b = [7, 9], k = 4
Output: 7
Explanation: The final sorted array would be:
[2, 3, 6, 7, 9]
The 4th element is 7Constraints:
- 1 ≤ m, m ≤ 10^4
- 0 ≤ arr1[i], arr2[i] < 10^9
- 1 ≤ k ≤ m + n
Different Approaches
1️⃣ Binary Search
Intuition:
On observation it can be found that this problem is a variant of another problem Median of two sorted arrays.
So, the entire logic of the optimal solution will remain the same here with just few changes; instead of finding the median, the kth element of two sorted arrays will be determined.
Observation:
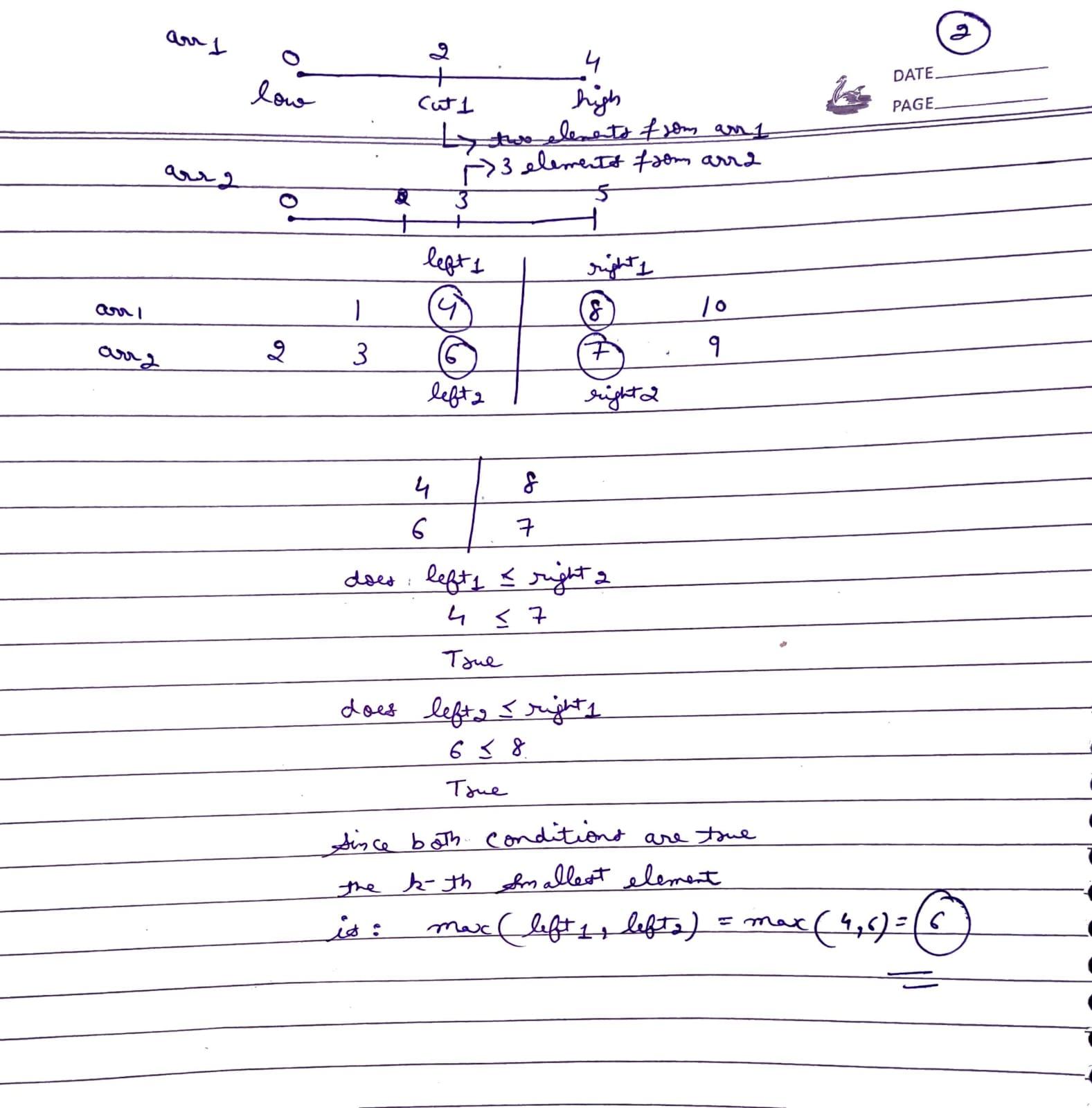
Assume, m = size of arr1[] and n = size of arr2[]. The median creates a partition on the final merged array, dividing it into two halves with approximately equal sizes, around (m+n) / 2. It was also discussed that these halves must be unique in a valid merged array. The approach involved forming the correct unique left half, assuming it contains x elements from arr1[] and ((m+n)/2)-x elements from arr2[], where x ranges from 0 to min(m, n). For each value in this range, the configuration of the left half was validated using the condition l1 <= r2 && l2 <= r1, where l1, r1 are variables referring to elements from arr1[], and l2, r2 refer to elements from arr2[].
The same approach will be used with some minor changes in the values. The changes will be as follows:
The size of the left half will be k: Here, the median does not need to be found; instead, the k-th element is sought. Therefore, the partition will be placed after the k-th element. Consequently, the size of the left half will be k instead of (m+n)/2. For example,
+-----+-----+-----+-----+
arr1 = | 2 | 3 | 6 | 15 |
+-----+-----+-----+-----+
+-----+-----+-----+-----+-----+-----+
arr2 = | 1 | 3 | 4 | 7 | 10 | 12 |
+-----+-----+-----+-----+-----+-----+
k = 4, means the 4th element
+---+---+---+---+---+---+---+---+---+---+
mergedArr = | 1 | 2 | 3 | 3 | 4 | 6 | 7 | 10| 12| 15|
+---+---+---+---+---+---+---+---+---+---+
^
|
k
+---+---+---+---+ +---+---+---+---+---+---+
| 1 | 2 | 3 | 3 | | 4 | 6 | 7 | 10| 12| 15|
+---+---+---+---+ +---+---+---+---+---+---+
|_______________| |_______________________|
Left Half Right HalfRange of x:
- The maximum possible value of
xis determined by aiming to construct the left subarray of sizek. Therefore, the maximum possible value should bek. However, ifarr1[]has a size ofn1andn1 < k, then the maximum possible value will ben1. Thus after generalization, the maximum value will be determined bymin(k, n1), wheren1denotes the size of the smaller array, withn1 = min(m, n). - The minimum possible value of x (i.e., the number of elements to be taken from arr1[]) can be understood using an example. Given arr1[] size m = 6, arr2[] size n = 5, and k = 7, the minimum value of x should be 2. When constructing an array of size 7, and considering that the maximum number of elements we can take from arr2[] is 5, a minimum of 2 elements must be taken from arr1[].
- Therefore, the minimum possible value should be ( k - n2 ), where ( n2 ) represents the size of the not-considered array (i.e., the bigger array). However, if ( k < n2 ), ( k - n2 ) will be negative. To handle this case, the minimum value is considered as ( max(0, k - n2) ), where ( n2 ) denotes the size of the bigger array, with ( n2 = max(m, n) ).
- The new range of x is determined by [max(0, k-n2), min(k, n1)], where n1 denotes the size of the smaller array, and n2 denotes the size of the bigger array. Here, n1 is defined as min(m, n) to optimize the time complexity by considering the array with the smaller length. Binary search will be applied within this new range.
Note: The answer will always be max(l1, l2) as the kth element will be the maximum element of the left half.
The rest of the process will be as similar to the one used in the problem, Median of 2 sorted arrays.
Approach:
- First, make sure that the
arr1is the smaller array. If not by default, just swap the arrays. Our main goal is to consider the smaller array asarr1[]. Calculate the length of the left half asleft = k. - Initialize two pointers:
lowandhigh,lowwill point tomax(0, k-n2), and thehighwill point tomin(k, n1)(i.e.n1is the size of the smaller array,n2is the size of the bigger array). Calculate the‘mid1’i.e.xand‘mid2’i.e. [left-x]. Now, inside the loop, calculate the value of‘mid1’using the following formula,mid1 = (low+high) // 2( ‘//’ refers to integer division) andmid2 = left-mid1. - Calculate
l1,l2,r1, andr2: Generally,l1 = arr1[mid1-1]l2 = arr2[mid2-1]r1 = arr1[mid1]r2 = arr2[mid2]. The possible values of‘mid1’and‘mid2’might be0andn1andn2respectively. So, to handle these cases, store some default values for these four variables. The default value forl1andl2will beINT_MINand forr1andr2, it will beINT_MAX. - Eliminate the halves based on the following conditions:
- If the condition
l1 <= r2andl2 <= r1and is satisfied, the answer is found. The maximum ofl1 and l2is returned. - If
l1>r2, indicating that more elements fromarr1[]have been considered than necessary, fewer elements fromarr1[]and more fromarr2[]are required. In such a scenario, smaller values ofxshould be tried. To achieve this, the right half is eliminated (highis set tomid1 - 1). - If
l2>r1, implying that more elements fromarr2[]have been considered than necessary, fewer elements fromarr2[]and more fromarr1[]are required. In such a scenario, larger values ofxshould be tried. To achieve this, the left half is eliminated (lowis set tomid1 + 1).
- If the condition
- Finally, when the loop terminates, include a dummy return statement just to avoid warnings or errors.



Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int kthElement(vector<int>& a, vector<int>& b, int k) {
int m = a.size();
int n = b.size();
// Ensure a is smaller array for optimization
if (m > n) {
// Swap a and b
return kthElement(b, a, k);
}
// Length of the left half
int left = k;
// Apply binary search
int low = max(0, k - n), high = min(k, m);
while (low <= high) {
int mid1 = (low + high) >> 1;// similar to (low + high)/2
int mid2 = left - mid1;
// Initialize l1, l2, r1, r2
int l1 = (mid1 > 0) ? a[mid1 - 1] : INT_MIN;
int l2 = (mid2 > 0) ? b[mid2 - 1] : INT_MIN;
int r1 = (mid1 < m) ? a[mid1] : INT_MAX;
int r2 = (mid2 < n) ? b[mid2] : INT_MAX;
// Check if we have found the answer
if (l1 <= r2 && l2 <= r1) {
return max(l1, l2);
}
else if (l1 > r2) {
// Eliminate the right half
high = mid1 - 1;
}
else {
// Eliminate the left half
low = mid1 + 1;
}
}
// Dummy return statement
return -1;
}
};
int main() {
vector<int> a = {2, 3, 6, 7, 9};
vector<int> b = {1, 4, 8, 10};
int k = 5;
//Create an instance of Solution class
Solution solution;
//Print the answer
cout << "The " << k << "-th element of two sorted arrays is: "
<< solution.kthElement(a, b, k) << '\n';
return 0;
}
Complexity Analysis:
- Time Complexity:
O(log(min(M, N))), whereMandNare the sizes of the two given arrays. As, binary search is being applied on the range[max(0, k - N2), min(k, N1))]. The range length ≤ min(M, N). - Space Complexity:
O(1)

