Problem Statement

Given an array of integers nums and an integer k, return the total number of subarrays whose XOR equals to k.

Examples

Example 1:

Input: nums = [4, 2, 2, 6, 4], k = 6
Output: 4

Explanation: The subarrays having XOR of their elements as 6 are
[4, 2], [4, 2, 2, 6, 4], [2, 2, 6], and [6]

Example 2:

Input: nums = [5, 6, 7, 8, 9], k = 5
Output: 2

Explanation: The subarrays having XOR of their elements as 5 are
[5] and [5, 6, 7, 8, 9]

Different Approaches

1️⃣ Brute Force Approach

Intuition:

We will check the XOR of every possible subarray and count how many of them are equal to k. To do this, use three nested loops. The first two loops (let's call them i and j) will iterate over every possible starting and ending index of a subarray. In each iteration, the subarray range will be from index i to index j. Using another loop, calculate the XOR of the elements in the subarray [i...j]. Count the number of subarrays where the XOR is equal to k.

Note: Select every possible subarray using two nested loops, and for each subarray, calculate the XOR of all its elements using another loop.

Approach:

1. First, run a loop (let's call it i) that selects every possible starting index of the subarray. The starting indices can range from index 0 to n−1 (where n is the size of the array). Inside this loop, run another loop (let's call it j) that signifies the ending index of the subarray. For each subarray starting from index i, the ending index can range from i to n−1.
2. For each subarray from index i to j (i.e., arr[i...j]), run another loop to calculate the XOR of all the elements in that subarray.
3. If the XOR equals k, increase the count by 1.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to count the number of subarrays with XOR k
    int subarraysWithXorK(vector<int>& nums, int k) {
        int n = nums.size(); 
        int cnt = 0;

        // Step 1: Generate subarrays
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) {
                int xorr = 0;
                /* Step 2: Calculate XOR of 
                   all elements in the subarray */
                for (int K = i; K <= j; K++) {
                    xorr = xorr ^ nums[K];
                }
                // Step 3: Check XOR and count
                if (xorr == k) cnt++;
            }
        }
        return cnt;
    }
};

int main() {
    vector<int> a = {4, 2, 2, 6, 4}; 
    int k = 6; 

    // Create an instance of the Solution class
    Solution solution;

    // Function call to get the result
    int ans = solution.subarraysWithXorK(a, k);
  
    cout << "The number of subarrays with XOR k is: " << ans << "\n";
    return 0;
}

Complexity Analysis:

• Time Complexity: O(n^3), where n is the size of the array.
• Space Complexity: O(1)

2️⃣ Better Approach

Intuition:

If we carefully observe, we can notice that to get the XOR of the current subarray, we just need to XOR the current element (i.e., arr[j]) with the XOR of the previous subarray (i.e., arr[i...j-1]). Assume the previous subarray is arr[i...j-1] and the current subarray is arr[i...j]. The XOR of arr[i...j] can be calculated as (XOR of arr[i...j-1]) ^ arr[j]. This approach allows us to remove the third loop, and calculate the XOR while moving the j pointer.

Approach:

1. First, run a loop (let's call it i) that selects every possible starting index of the subarray. The starting indices can range from index 0 to n−1 (where n is the size of the array). Inside this loop, run another loop (let's call it j) that signifies the ending index of the subarray. For each subarray starting from index i, the ending index can range from i to n−1.
2. For each subarray from index i to j, calculate the XOR of all the elements in that subarray by simply doing XOR operation on the previous XOR and the element at j index.
3. If the XOR equals k, increase the count by 1.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to count the number of subarrays with XOR k
    int subarraysWithXorK(vector<int>& nums, int k) {
        int n = nums.size(); 
        int cnt = 0;

        // Step 1: Generate subarrays
        for (int i = 0; i < n; i++) {
            int xorr = 0;
            for (int j = i; j < n; j++) {
                /* Step 2: Calculate XOR of
                   all elements in the subarray */
                xorr = xorr ^ nums[j];

                // Step 3: Check XOR and count
                if (xorr == k) cnt++;
            }
        }
        return cnt;
    }
};

int main() {
    vector<int> a = {4, 2, 2, 6, 4}; 
    int k = 6; 

    // Create an instance of the Solution class
    Solution solution;
    // Function call to get the result
    int ans = solution.subarraysWithXorK(a, k);

    
    cout << "The number of subarrays with XOR k is: " << ans << "\n";
    return 0;
}

Complexity Analysis:

• Time Complexity: O(n^2), where n is the size of the array.
• Space Complexity: O(1)

3️⃣ Optimal Approach

Intuition:

In this approach, try to utilize the concept of prefix XOR to solve this problem. The prefix XOR of a subarray ending at index i is simply the XOR of all the elements from the start of the array up to index i.

Observation:

To find subarrays with XOR equal to k, let the prefix XOR of the subarray ending at index i be xr. For a subarray to have XOR k, the prefix XOR of the earlier part of the array must be xr XOR k.

• If the XOR of the whole subarray up to index i is r.
• And removing the prefix part with XOR xr ^ k
• The remaining part will have XOR k.

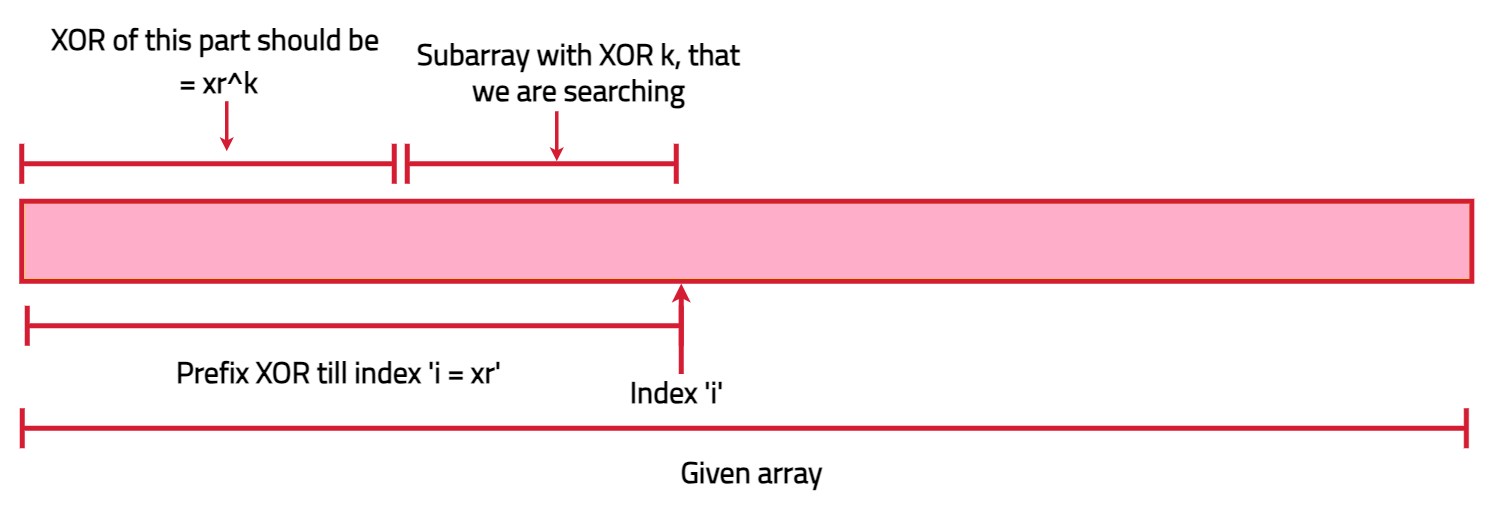
Instead of directly searching for subarrays with XOR k, we use a map to count subarrays with prefix XOR xr XOR k. The map stores each prefix XOR and its count. At each index i, we check the map for xr XOR k and add the count to our result. We repeat this for all indices from 0 to n-1. This approach efficiently finds the number of subarrays with XOR k using the prefix XOR concept and a map.

Approach:

The steps are as follows:

1. First start by declaring a map to store the prefix XORs and their counts, and set the value of 0 as 1 in the map. This setup is crucial because it helps us handle cases where the prefix XOR itself equals the target value k.
2. Run a loop from index 0 to n-1 (where n is the size of the array). For each index i, XOR the current element arr[i] with the existing prefix XOR. Then calculate the required prefix XOR xr^ k to check its occurrence.
3. Now, add the occurrence of the prefix XOR xr ^ k from the map to our answer. This gives the count of subarrays that have the desired XOR value k. Finally, store the current prefix XOR xr in the map, increasing its occurrence by 1 to keep track of its count for future subarrays.

Question: Why set the value of 0 beforehand?

To understand this, consider the array [3, 3, 1, 1, 1] with k = 3. At index 0, the total prefix XOR is 3, and k is also 3. So, the prefix XOR xr XOR k will be 3 XOR 3 = 0. If the value 0 is not previously set in the map, we will add 0 to our answer, incorrectly indicating that no subarray with XOR 3 has been found. However, index 0 itself is a subarray with XOR k = 3. Setting the value of 0 as 1 in the map beforehand avoids this issue.

Code:

class Solution
{
public:
    int subarraysWithXorK(vector<int>& nums, int k)
    {
        int n = nums.size(); 
        int xr = 0;
        map<int, int> mpp; 
        // setting the value of 0.
        mpp[xr]++; 
        int cnt = 0;

        for (int i = 0; i < n; i++) {
            // prefix XOR till index i:
            xr = xr ^ nums[i];

            // By formula: x = xr^k:
            int x = xr ^ k;

            // add the occurrence of xr^k to the count:
            cnt += mpp[x];

            // Insert the prefix xor till index i into the map:
            mpp[xr]++;
        }
        return cnt;
    }
};

Complexity Analysis:

• Time Complexity: O(N) or O(NxlogN), where N is the size of the array. If we use an unordered_map in C++, the time complexity is O(N). However, with a map data structure, the time complexity is O(NxlogN). In the worst case for an unordered_map, the searching time can increase to O(N), making the overall time complexity O(N2).
• Space Complexity: O(N), as we are using a map data structure.