Problem Statement
Given an integer n, there is a staircase with n steps, starting from the 0th step. Determine the number of unique ways to reach the nth step, given that each move can be either 1 or 2 steps at a time.
Examples
Example 1:
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step (1 step from 0th to 1th step, another for 1st to second step)
2. 2 steps (Directly climbing from 0th step to 2nd step)Example 2:
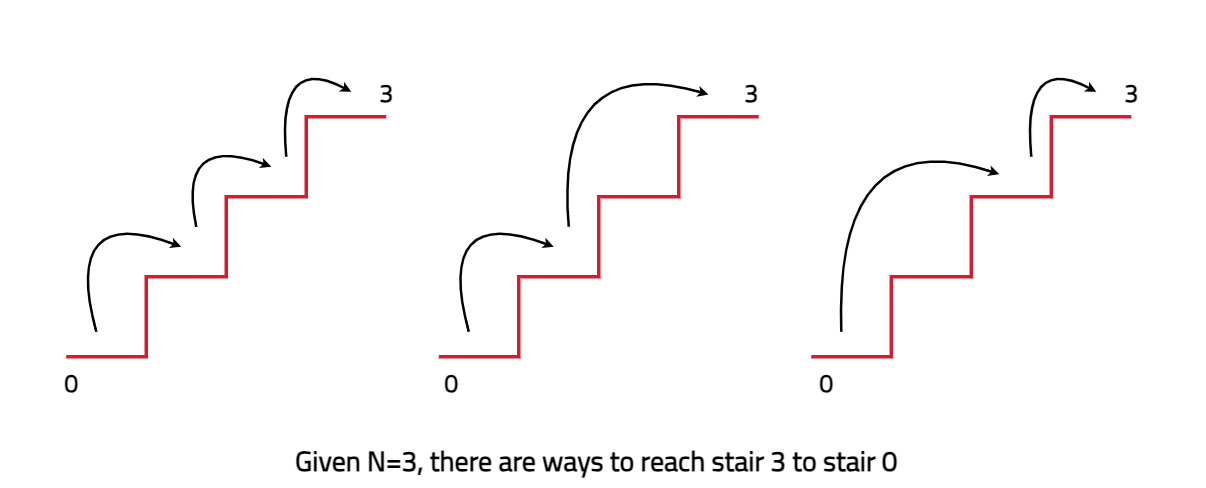
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1 step + 1 step + 1 step
1 step + 2 step
2 step + 1 stepTheory
How to Identify a Problem to be Recursion Based?
If a problem includes:
- Problem asking for count the total number of ways. Like Try all possible ways. (
count) - Given there are multiple ways of performing a task, and it is asked which would give the minimum or maximum output. (
best way)
then we are tend to apply the recursion. Once recursion solution is obtained, it can be converted into a dynamic programming approach.
For instance
for this problem, when n = 3
1 1 1
0 -> 1 -> 2 -> 3
2 1
0 ------> 2 -> 3
1 2
0 -> 1 ------> 3
This problem is giving us an idea which is try all possible
ways, thus this problem is candiate of recursion.Recursive Solution:
The simplest way to solve the climbing stairs is by using recursion. The recursion formula for this problem is:
ways(n) = ways(n-1) + ways(n-2)
where ways(0) = 1 and ways(1) = 1
We count starting point as 1 way. That is base case and it's obvious that we have only one way to reach stair 1, because we can make 1 step or 2 steps from the starting point.Let's consider the recursive approach first. When you're at step n, you can either reach it from step n-1 by taking one step, or from step n-2 by taking two steps. Therefore, the total number of ways to reach step n is the sum of the ways to reach steps n-1 and n-2.

int climbStairs(int n) {
if (n <= 1)
return 1;
return climbStairs(n - 1) + climbStairs(n - 2);
}
Although this recursive solution is simple, it has exponential time complexity of O(2^n), making it impractical for large values of n.
Different Approaches
The intuition behind the dynamic programming solution lies in the fact that to reach step n, you have two choices:
- You can reach it from step n-1 by taking one step.
- You can reach it from step n-2 by taking two steps.
So, the total number of ways to reach step n is the sum of the ways to reach steps n-1 and n-2. This is a classic example of the Fibonacci sequence, where F(n) = F(n-1) + F(n-2).
1️⃣ Recursion
The problem statement asks to count the total ways one can jump from 0th step to the nth step by jumping either 1 or 2 steps at a time. Since the question requires counting total ways, recursion can be applied, and eventually, this problem can also be solved using dynamic programming.
How to Write Recurrence Relation:
Once the problem has been identified, the following three steps comes handy in solving the problem:
- Try to represent the problem in terms of indexes.
- Try all possible choices/ways at every index according to the problem statement.
- If the question states "
count all the ways”, then thesum of all choices/waysshould be returned. If the question asks to find "the maximum/minimum", then the choice/way with themaximum/minimumoutput should be returned.
Solution using Recursion:
- In recursion, top-down approach is followed, so try getting the answer that is required, then go to the base case and come back.
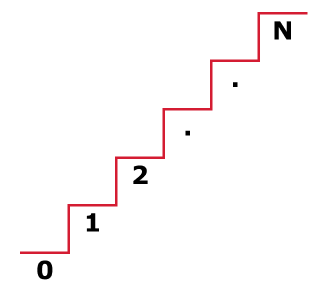
- To represent the problem in terms of indices, assume
nstairs as indices from0toN. The recursive call will basically return all the ways to reach thenthstep.
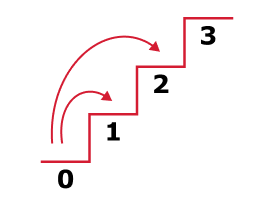
- In order to consider all possible actions at an index, the choices available are either to jump
1step or2steps, so proceed accordingly.
- Now, to count all the ways, return the sum of all the choices in our recursive function.
/*It is pseudocode and not tied to
any specific programming language.*/
f(n){
oneStep = f(n-1)
twoStep = f(n-2)
return oneStep + twoStep
}- The base case would be, when the
n = 0, it means, the starting and ending steps are the same. So, there is just one way possible and that will be to stand there as it is. - Edge Case: When
n = 1andf(n-2)has been called, we will reach stair-1, which is not valid stair. Therefore, an additional edge case is added to return1(the only way) whenn = 1.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Function to count total ways to reach nth stair
int climbStairs(int n) {
// Base case
if (n == 0) return 1;
if (n == 1) return 1;
// Taking 1 step at a time
int oneStep = climbStairs(n-1);
// Taking 2 steps at a time
int twoSteps = climbStairs(n-2);
// Return total ways
return oneStep + twoSteps;
}
};
int main() {
int n = 3;
// Create an instance of Solution class
Solution sol;
// Print the answer
cout << "The total number of ways: " << sol.climbStairs(n) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(2^N), whereNis the given number of stairs. The number of recursive calls roughly follows a Fibonacci-like sequence, whereclimbStairs(n)is approximately2^N. This is because each call branches into two more calls, leading to an exponential growth in the number of calls. - Space Complexity: The space complexity of this recursive approach is
O(n). This is because the maximum depth of the recursion stack can go up ton, due to the linear nature of the stack usage relative to the input sizen.
2️⃣ Memoization (Top-Down) DP Approach
As, the recursive solutions recalculate the same subproblems again and again, leading to inefficiencies, especially with larger inputs. Memoization addresses this by storing the results of already computed subproblems.
When a subproblem is encountered again, which is known as overlapping subproblem, instead of recalculating it, the precomputed result is simply retrieved from memory. This speeds up the computation and also reduces the time complexity significantly, often transforming an exponential-time recursive solution into a polynomial-time solution.
- Memoization tends to store the value of subproblems in some map/ table. As, here we have only one parameter in recursive function, so we can create an 1D array to store the values of subproblems.
- Declare an Array dp[] of Size n+1: Here, n is the parameter or size of the problem, as the highest number of subproblems can be n+1(including 0 as well). It represents the solution to the subproblem for any given index. Initially, fill the array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
//Helper function to apply memoization
int func(int n, vector<int> &dp) {
// Base condition
if (n <= 1) {
return 1;
}
// Check if the subproblem is already solved
if (dp[n] != -1) {
return dp[n];
}
// Return the calculated value
return dp[n] = func(n-1, dp) + func(n-2, dp);
}
public:
// Function to count total ways to reach nth stair
int climbStairs(int n) {
// Initialize dp vector with -1
vector<int> dp(n + 1, -1);
return func(n, dp);
}
};
int main() {
int n = 5;
// Create an instance of Solution class
Solution sol;
// Print the answer
cout << "The total number of ways: " << sol.climbStairs(n) << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(N), whereNis the given number of stairs. This is because we perform a linear number of operations relative to the input size n. - Space Complexity:
O(N) + O(N), We are using a recursion stack spaceO(N)and an array (againO(N)). Therefore total space complexity will beO(N) + O(N) ≈ O(N).
3️⃣ Tabulation (Bottom-Up) DP Approach
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Bottom-Up Approach in Tabulation: Tabulation involves solving a problem by building a solution from the bottom up. This means start with the smallest subproblems and iteratively compute solutions for larger subproblems until the desired solution has been found.
- Declare an Array dp[] of Size n+1: Here, n is the parameter or size of the problem. It represents the solution to the subproblem for any given index.
- Setting Base Cases in the Array: In the recursive code, we knew the answer for base cases, similarly if we are computing in tabulation, we definitely know that the answer for
dp[0] = 0 and dp[1] = 1. - Iterative Computation Using a Loop: Set an iterative loop that traverses the array (
from index 2 to n). To compute the solution for larger values, use a loop that iterates from the smallest subproblem up to n. The current value(dp[i]) represents the subproblem and by the recurrence relation it is obvious that it is sum of previous two values, for every index(i) set its value asdp[i-1] + dp[i-2]. - Returning the last element: The last element of the
dparray is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Function to count total ways to reach nth stair
int climbStairs(int n) {
//Declare dp array of size n+1
vector<int> dp(n + 1, -1);
//Insert the values of base conditions
dp[0] = 1;
dp[1] = 1;
//Iterate and update every index of dp array
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
//Return the answer
return dp[n];
}
};
int main() {
int n = 3;
// Create an instance of Solution class
Solution sol;
// Print the answer
cout << "The total number of ways: " << sol.climbStairs(n) << endl;
return 0;
}Complexity Analysis:
- Time Complexity:
O(N), whereNis the given number of stairs. This is because we perform a linear number of operations relative to the input size N. - Space Complexity:
O(N), an additional arraydpof sizen + 1is used to store intermediate results. Hence, the space complexity is O(N).
4️⃣ Space Optimized DP
If we observe the relation dp[i] = dp[i-1] + dp[i-2], we notice that to calculate the current value at index i, we only need the previous two values. Using an entire array for just two values seems overhead. Instead, the work can be done using two variables to store the previous two values, achieving O(1) space complexity. In each iteration, the current value and the variables containing previous values can be updated.
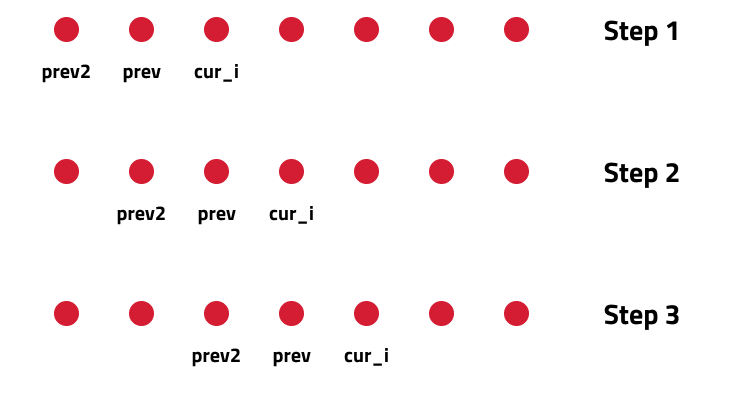
- In each iteration, cur_i is calculated and prev and prev2 are updated to become the next iteration's prev and prev2 respectively.
- After the iterative loop has ended, prev is returned as the answer.
for n = 4;
1. Initialize prev and curr to 1:
prev = 1
curr = 1
2. Start the loop from 2 to n:
Iteration 1 (i = 2):
temp = curr = 1
curr = prev + curr = 1 + 1 = 2
prev = temp = 1
Iteration 2 (i = 3):
temp = curr = 2
curr = prev + curr = 1 + 2 = 3
prev = temp = 2
Iteration 3 (i = 4):
temp = curr = 3
curr = prev + curr = 2 + 3 = 5
prev = temp = 3
Finally, return curr = 5, which represents the number of ways to climb 4 stairs.Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Function to count total ways to reach nth stair
int climbStairs(int n) {
/*Initialize two variables to
store previous results*/
int prev2 = 1;
int prev = 1;
//Iterate and update the variables
for (int i = 2; i <= n; i++) {
int cur_i = prev2 + prev;
prev2 = prev;
prev = cur_i;
}
//Return the answer as prev
return prev;
}
};
int main() {
int n = 3;
// Create an instance of Solution class
Solution sol;
// Print the answer
cout << "The total number of ways: " << sol.climbStairs(n) << endl;
return 0;
}Complexity Analysis:
- Time Complexity:
O(N), whereNis the given number of stairs. This is because we perform a linear number of operations relative to the input size n. - Space Complexity:
O(1). As no extra space is being used here.

