Problem Statement

Sometimes, it becomes essential to check whether a specific bit is set (equals 1) or not in a binary representation of a number. Let's consider the problem of determining if the k'th bit is set in a given number. Given an integer num and a positive integer k, our task is to find out whether the k'th bit is set or not.

Understanding the Problem

Consider the following scenario:

Input: num = 21, k =3

Our goal is to check if the 3rd bit (from the right, considering 0-based index) is set in the binary representation of 21.
Binary representation of 21: 10101.
Here, the 3rd bit is set (equals 0). So, for the given input, the expected output should be false.

Examples

Example 1:

Input: n = 5, k = 0
Output: true

Explanation: Binary of 5 = 0000...0101 -> 0th bit is 1

Example 2:

Input: n = 5, k = 1
Output: false

Explanation: Binary of 5 = 0000...0101 -> 1st bit is 0

Example 3:

Input: n = 5, k = 2
Output: true

Explanation: Binary of 5 = 0000...0101 -> 2nd bit is 1

Different Approaches

1️⃣ Bit Manipulation (bitwise AND)

To solve this problem efficiently, we can use bitwise AND operation (&) along with the left shift operation (<<).

The idea is to create a mask with the k'th bit set and then perform a bitwise AND operation with the given number. If the result is not zero, then the k'th bit is set; otherwise, it is not set.

Approach:

1. Create a mask: 1 << k → This shifts 1 to the k-th position.
2. Perform n & (1 << k):
   • If result ≠ 0 → bit is set.
   • If result == 0 → bit is not set.

Edge Case:

• If k is negative or too large (beyond 31 or 63 depending on the system), handle gracefully.

Bit Position:

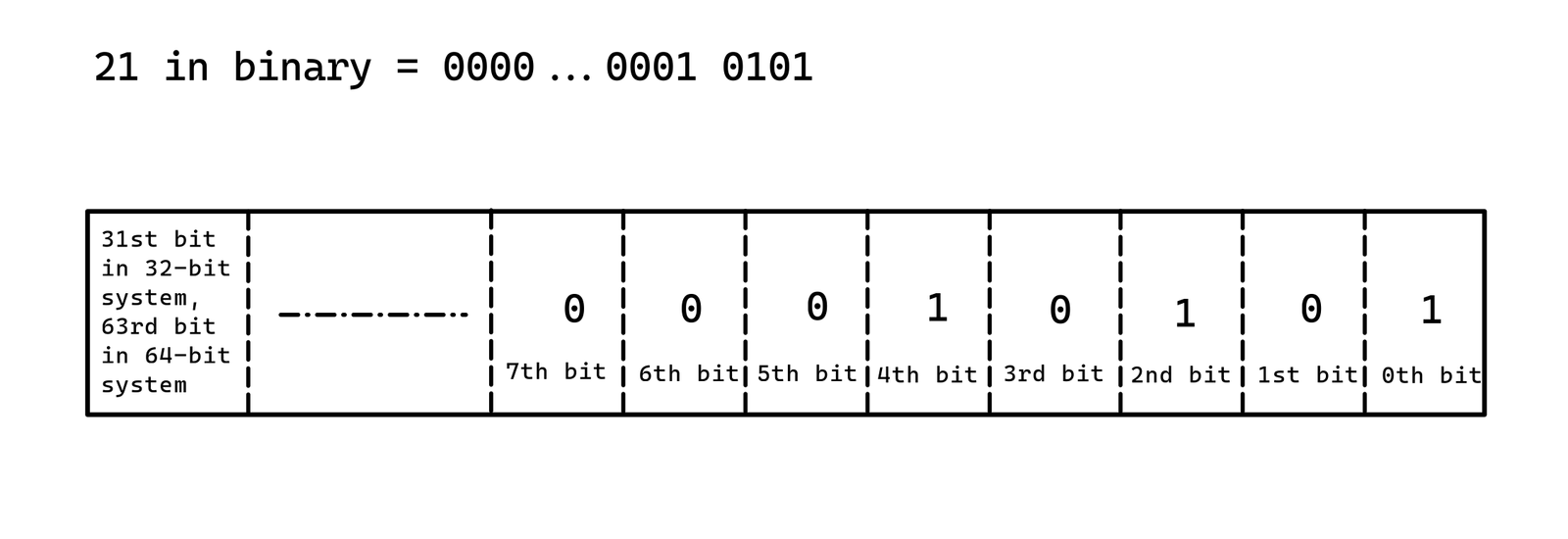
Code:

#include <iostream>

bool isKthBitSet(int num, int k) {
    // Create a mask with the k'th bit set
    int mask = 1 << k;

    // Perform bitwise AND operation
    // If result is not zero, k'th bit is set
    return (num & mask) != 0;
}

int main() {
    // Example usage
    int num = 21, k = 3;
    
    // Check if the k'th bit is set
    if (isKthBitSet(num, k)) {
        std::cout << "The " << k << "'th bit is set in " << num << std::endl;
    } else {
        std::cout << "The " << k << "'th bit is not set in " << num << std::endl;
    }

    return 0;
}

// Output
21 in binary = 0001 0101
The 3'th bit is not set in 21

Complexity Analysis:

• Time Complexity:O(1) Each operation is constant time.
• Space Complexity:O(1) No extra space used.